Предмет: Алгебра,
автор: olegkiricuk90
знайдіть усі цілі розв'язки нерівності. 2x²+x-6≤0
Приложения:
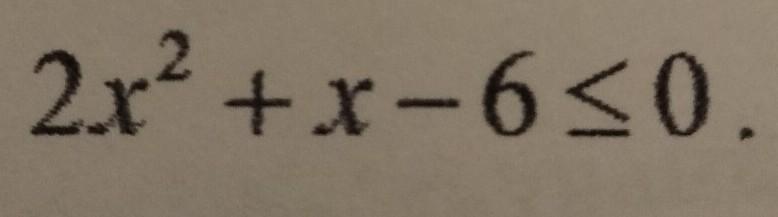
Ответы
Автор ответа:
3
+ + + + + [- 2] - - - - - [1,5] + + + + +
////////////////////
Автор ответа:
0
Ответ: -2;-1;0;1
Объяснение:
По Виета корни левой части. т.е. квадратного уравнения х=1.5. х=-2
решим неравенство методом интервалов
____-2________1.5_______
+ - +
х∈[-2;1.5] целые решения -2;-1;0;1
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Aliyaimamova
Предмет: Українська мова,
автор: AnutochkaSuper
Предмет: Українська мова,
автор: loglady002
Предмет: Математика,
автор: byckovam950