Question

Очень прошу помочь всех, кто знает геометрию.

Решить практическую задачу на экстремум.
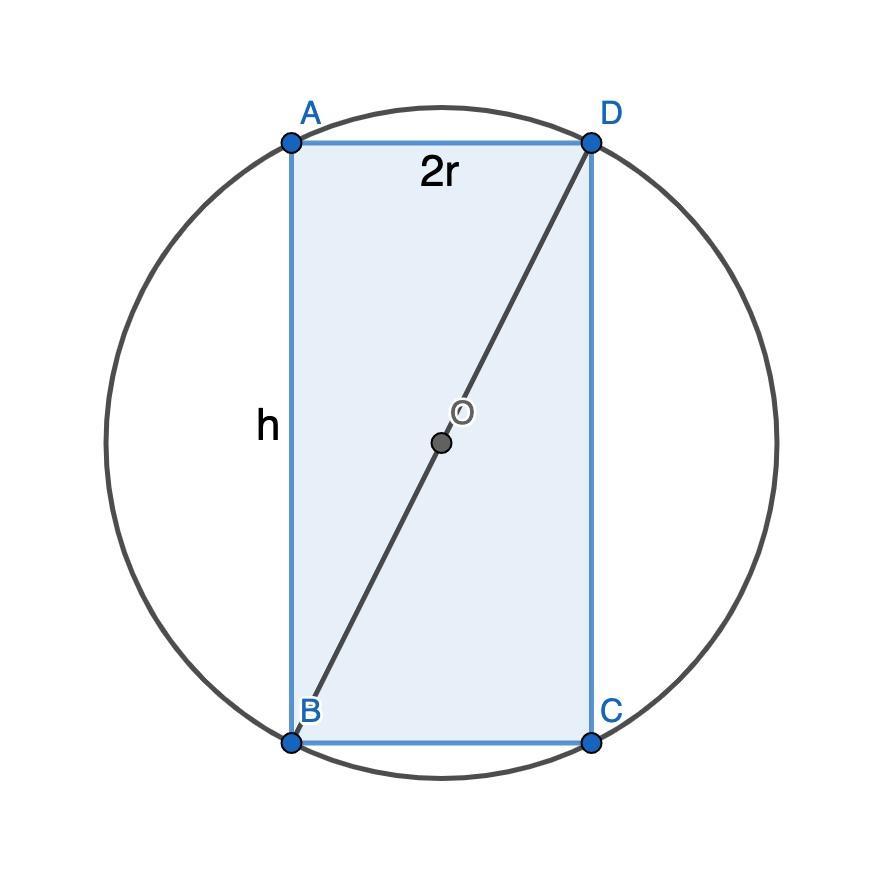
Среди цилиндров вписанных в шар единичного радиуса, найти цилиндр с максимальным объемом.​

Answer 1

Ответ:

Цилиндр с радиусом основания $r=\sqrt{\dfrac{2}{3}}$, высотой $h=\dfrac{2\sqrt{3}}{3}$

Объяснение:

Рассмотрим осевое сечение цилиндра и шара. Получаем прямоугольник ABCD, вписанный в окружность единичного радиуса с центром O. Поскольку сечение осевое, то AD — это диаметр цилиндра (обозначим как 2r), а AB — высота (h). BD — это диаметр окружности, равный 2. Радиус цилиндра и его высота в таком случае связаны отношением $h^2+(2r)^2=2^2\Leftrightarrow h^2+4r^2=4$ (по теореме Пифагора). Выразим отсюда r²: $4r^2=4-h^2\Leftrightarrow r^2=\dfrac{4-h^2}{4}$.

Объём цилиндра находится по формуле $V=\pi r^2h$. Заменяя r², получаем $V=\pi h\cdot\dfrac{4-h^2}{4}=\dfrac{\pi}{4}(4h-h^3)$. Высота не может быть больше диаметра окружности и неположительным числом, поэтому 0 < h < 2.

Исследуем функцию объёма V(h) на минимумы и максимумы. Для этого возьмём производную:

$V'(h)=\dfrac{\pi}{4}(4-3h^2)$

Нули производной: $h=\pm\dfrac{2}{\sqrt{3}}$. Поскольку 0 < h < 2, подходит только $h=\dfrac{2}{\sqrt{3}}$. При $0Радиус цилиндра в таком случае равен [tex]r=\sqrt{\dfrac{4-h^2}{4}}=\sqrt{\dfrac{4-\dfrac{4}{3}}{4}}=\sqrt{\dfrac{2}{3}}$. Объём в таком случае равен $V=\pi r^2 h=\pi\cdot\dfrac{2}{3}\cdot\dfrac{2}{\sqrt{3}}=\dfrac{4\pi\sqrt{3}}{9}$.