Предмет: Алгебра,
автор: Аноним
СРОЧНО ПРОШУ 60 БАЛІВ НОМЕР 10.6 10.8
Приложения:
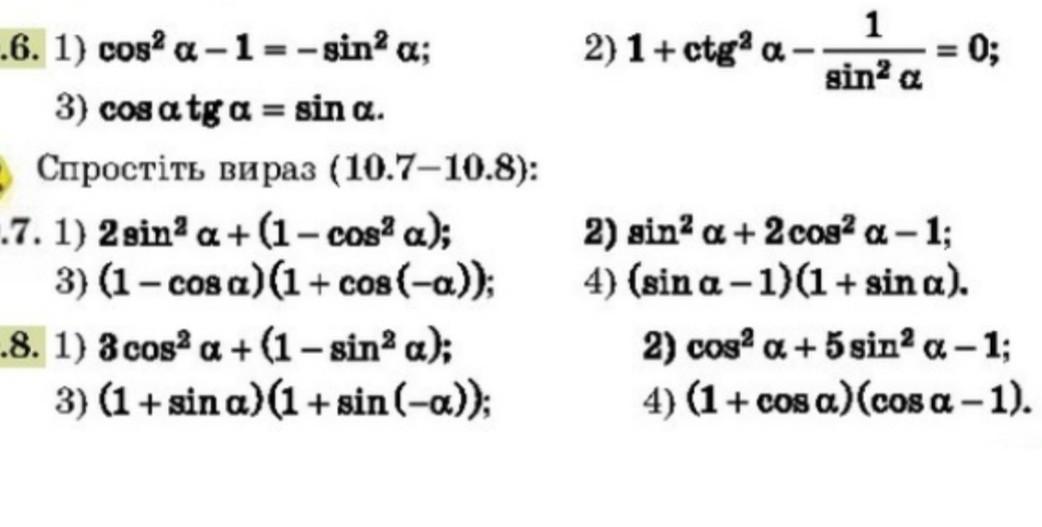
Ответы
Автор ответа:
1
Ответ: во вложении.
Объяснение:
там же
Приложения:

Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: savely3
Предмет: Окружающий мир,
автор: Алиса0707
Предмет: Русский язык,
автор: sharevma
Предмет: Математика,
автор: хакер12368
Предмет: Литература,
автор: gasangadzhieva39