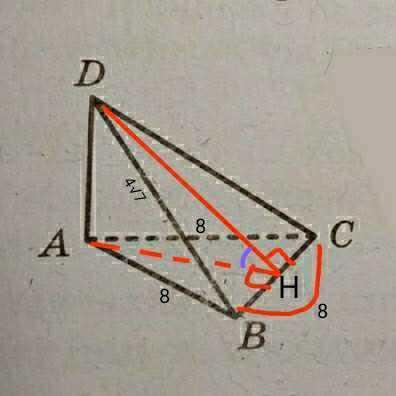
Помогите решить задачу
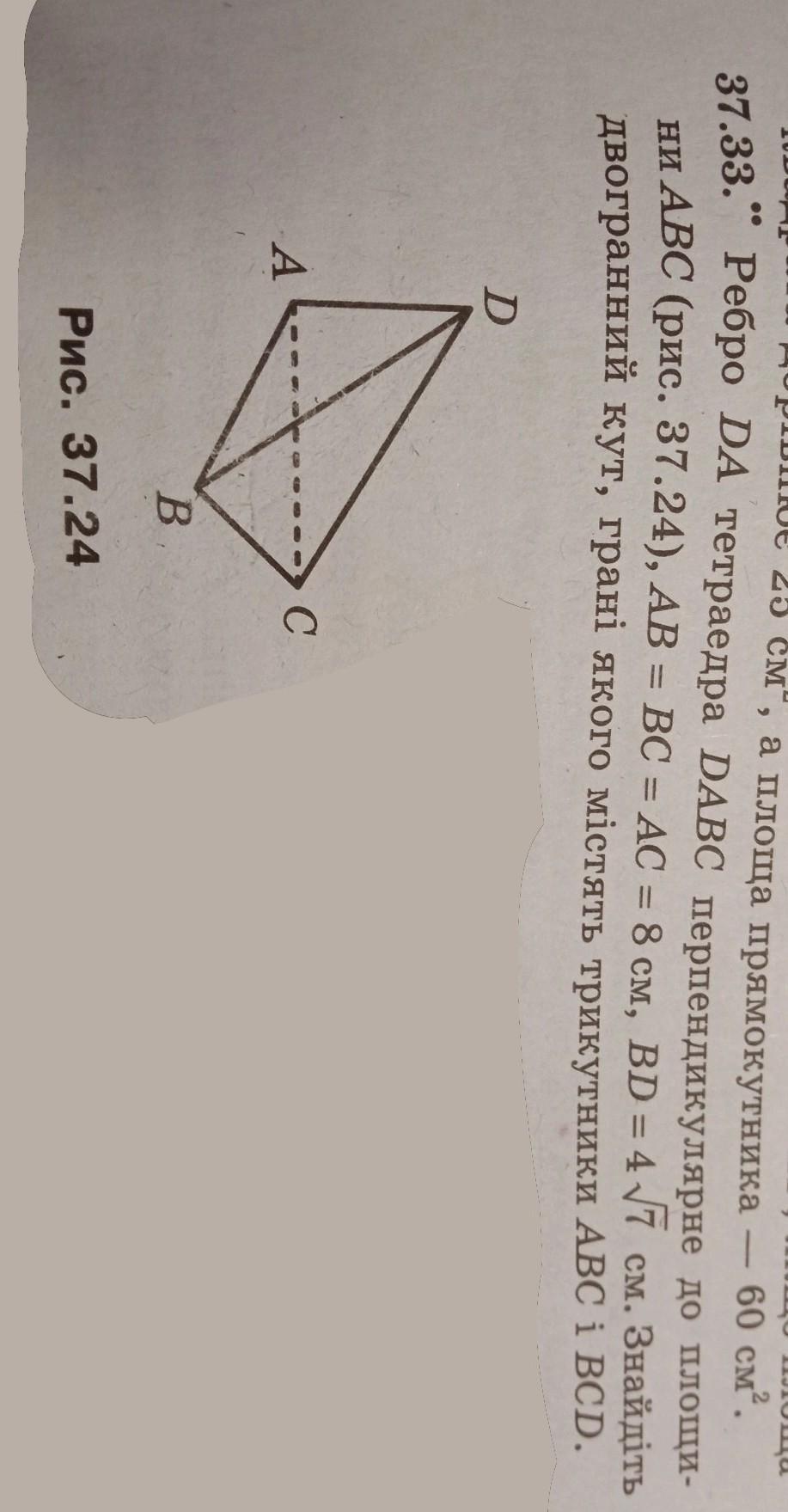
Ответы
Ответ: в тетраэдре ДАВС двухгранный ∠АНД=45°
Пошаговое объяснение: проведем 2 высоты: ДН в ΔВСД и АН в ΔАВС, и получим искомый двухгранный ∠АНД (отмечен на рисунке фиолетовым цветом). ΔАВС - равносторонний, поэтому высота АН будет также и медианой, которая делит сторону ВС пополам, поэтому ВН=НС=8:2=4см. ΔВСД - равнобедренный с основанием ВС (так как с равносторонним треугольником АВС у них совпадают вершины А и Д, и АВ=АС, то ВД=СД). В равнобедренном треугольнике высота, проведенная к основанию также является медианой, поэтому высота ДН тоже делит ВС пополам в точке Н. В данном случае основания высот обоих треугольников совпадают в одной точке Н. Найдем высоту АН в ΔАВС по формуле:
АН= ВС=
см
Высота ДН делит ΔВСД на 2 равных прямоугольных треугольника ВДН и СДН, в которых ДН, ВН и СН - катеты, а ВД и СД - гипотенузы. Найдем высоту ДН из ΔВДН по теореме Пифагора:
ДН²+ВН²=ВД² → ДН²=ВД²-ВН²=(4√7)²-4²=16*7-16=16(7-1)=16*6=96
ДН=√96=4√6см.
ΔАДН - прямоугольный, так как АД - перпендикуляр, АД и АН - катеты, а ДН - гипотенуза
Из ΔАДН найдем искомый ∠АНД через косинус угла. Косинус угла - это отношение прилежащего к углу катета к гипотенузе:
cosAHД=АН/ДН==45°