Question

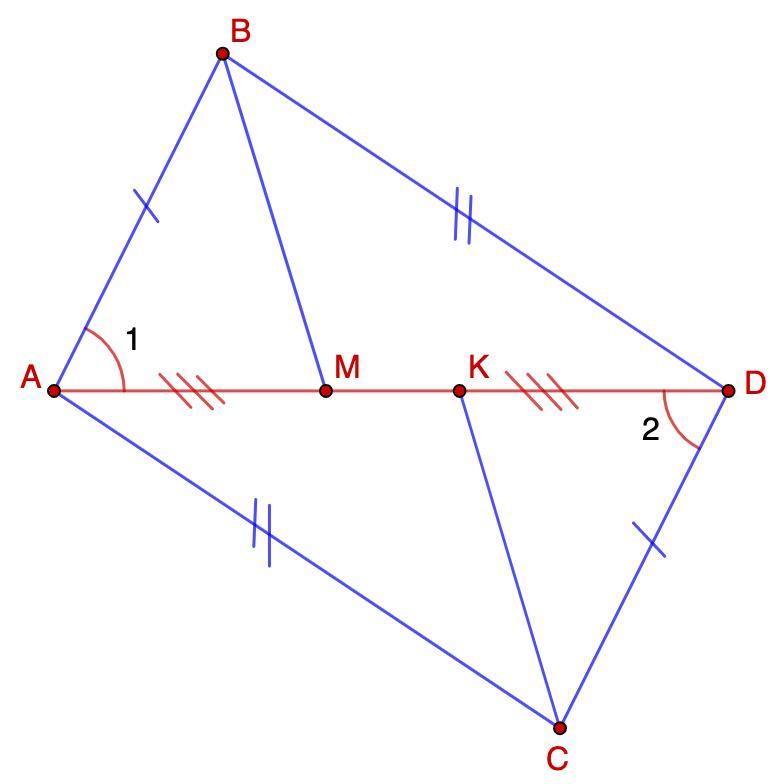
Даю 100 балів По різні сторони від прямої AD позначено точки B і C такі, що BA = CD і BD = CA . На відрізку AD узято точки M і K, при цьому AM = DK. Довести, що відрізки BM і CK рівні.​

Answer 1

Ответ:

Доказано, что отрезки ВС и СК равны.

Объяснение:

Требуется доказать, что отрезки ВМ и СК.

Дано: AD.

B ∉ AD; C ∉ AD;

BA = CD; BD = CA;

M ∈ AD; K ∈ AD;

AM = DK.

Доказать: ВМ = СК.

Доказательство:

1. Рассмотрим ΔABD и ΔADC.

BA = CD; BD = CA (условие);

AD - общая.

• Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

⇒ ΔABD = ΔADC.

• В равных треугольниках против равных сторон лежат равные углы.

⇒ ∠1 = ∠2.

2. Рассмотрим ΔАВМ и ΔKDC;

BA = CD; AM = DK (условие)

∠1 = ∠2 (п.1)

• Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

⇒ ΔАВМ = ΔKDC.

• В равных треугольниках против равных углов лежат равные стороны.

⇒ AM = DK.

Что и требовалось доказать.