Предмет: Геометрия,
автор: Кris2015
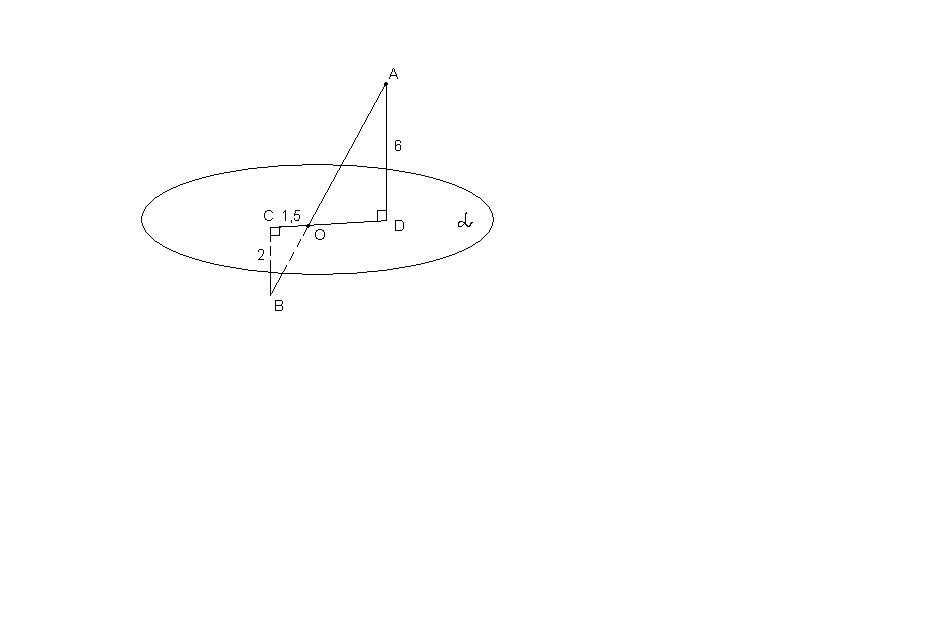
Отрезок AB пересекает некоторую плоскость в точке O. Прямые AD и BC, перпендикулярные к этой плоскости, пересекают ее в точках D и C соответственно. Найдите длину AB, если AD = 6см, BC = 2см, OC= 1,5см
Ответы
Автор ответа:
0
AD║BC как перпендикуляры к одной плоскости. Значит, точки А, В, С и D лежат в одной плоскости.
ΔВСО: ∠ВСО = 90°, по теореме Пифагора
ОВ = √(ВС² + ОС²) = √(4 + 2,25) = 2,5 см
ΔВСО подобен ΔADO по двум углам (углы при вершине О равны как вертикальные, ∠ВСО = ∠ADO = 90°), ⇒
АО/ОВ = AD/BC
AO = AD · OB / BC = 6 · 2,5 / 2 = 7,5 см
АВ = АО + ВО = 7,5 + 2,5 = 10 см
ΔВСО: ∠ВСО = 90°, по теореме Пифагора
ОВ = √(ВС² + ОС²) = √(4 + 2,25) = 2,5 см
ΔВСО подобен ΔADO по двум углам (углы при вершине О равны как вертикальные, ∠ВСО = ∠ADO = 90°), ⇒
АО/ОВ = AD/BC
AO = AD · OB / BC = 6 · 2,5 / 2 = 7,5 см
АВ = АО + ВО = 7,5 + 2,5 = 10 см
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: ruslan1906845
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: zyltrc7310
Предмет: Информатика,
автор: ima5555