Предмет: Математика,
автор: PLAY785
25 БАЛЛОВ РЕШИТЕ ПЖ 51 И 52 НОМЕР А И Б - БУДУ ОЧЕНЬ БЛАГОДАРЕН!!!!!!
Приложения:
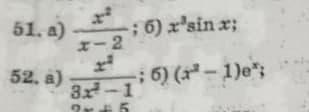
c4d4e4:
а что сделать то надо?
производную найти?
просто задали это я хз
а да производную надо
Ответы
Автор ответа:
0
проверяется производная произведения (u*v)'=u'v+uv' и производная частного (u/v)'=(u'v-uv')/v² . в 52. б) не четко виден показатель степени при х, вроде 2 или 3? я взял посложнее, т.е. 3
51. а) (х²/(х-2))'=(2x*(x-2)-1*x²)/(x-2)²=(2x²-4x-x²)/(x-2)²=(x²-4x)/(x-2)²;
б) (x³*sinx)=3x²*sinx+x³*cosx;
52а) (х²/(3х³-1))'=(2x*(3x³-1)-9х²*x²)/(3x³-1)²=(-2x-3x⁴)/(3x³-1)²;
б) (х³-1)еˣ=3х²*еˣ+(х³-1)еˣ=еˣ*(3х²+х₃-1)
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: мария120605
Предмет: Русский язык,
автор: NastyaKot123
Предмет: Русский язык,
автор: zverevanata201
Предмет: Математика,
автор: NyanKoshechka
Предмет: Алгебра,
автор: Кисса15