Question

Помогите пожуйлиста!!!!!!!!!аоаооаоаоаоао
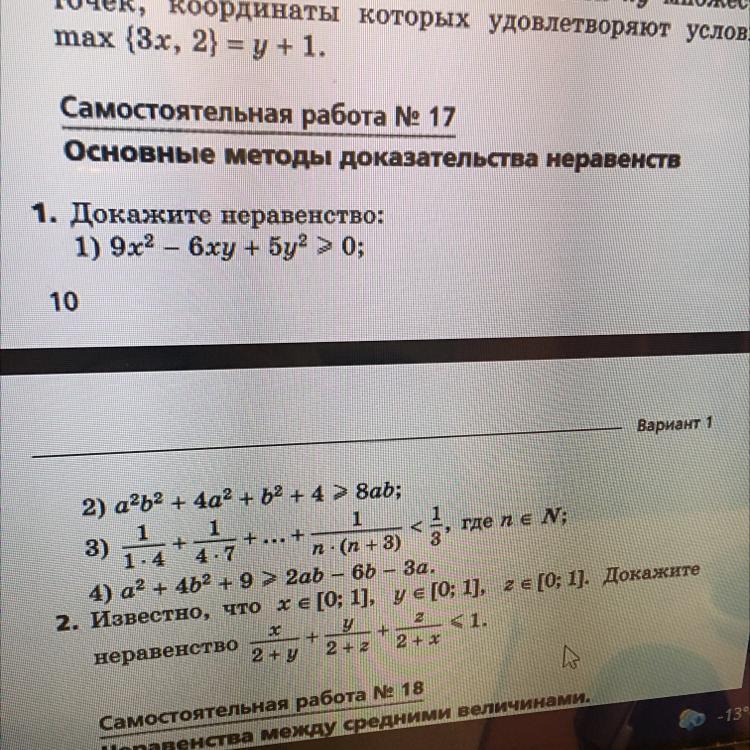
Докажите неравенства под номерами 3 и 4

Answer 1

3) Заметим, что $\dfrac{1}{j(j+3)} = \dfrac{1}{3}\left(\dfrac{1}{j}-\dfrac{1}{j+3}\right)$, а потому $\dfrac{1}{1\cdot 4}+\dfrac{1}{4\cdot 7}+\ldots +\dfrac{1}{n(n+3)} = \dfrac{1}{3}\left(\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\ldots+\dfrac{1}{n-3}-\dfrac{1}{n}+\dfrac{1}{n}-\dfrac{1}{n+3}\right) =\\ = \dfrac{1}{3}\left(1-\dfrac{1}{n+3}\right) < \dfrac{1}{3}$

4) Рассмотрим это неравенство как квадратное относительно $a$: $a^2-a(2b-3)+4b^2+6b+9 \geq 0$, поэтому необходимо доказать, что при любом $b$ дискриминант неположителен: $(2b-3)^2-4(4b^2+6b+9) = -12b^2-36b-27 = -3(2b+3)^2\leq 0$