Предмет: Геометрия,
автор: tarabrin63
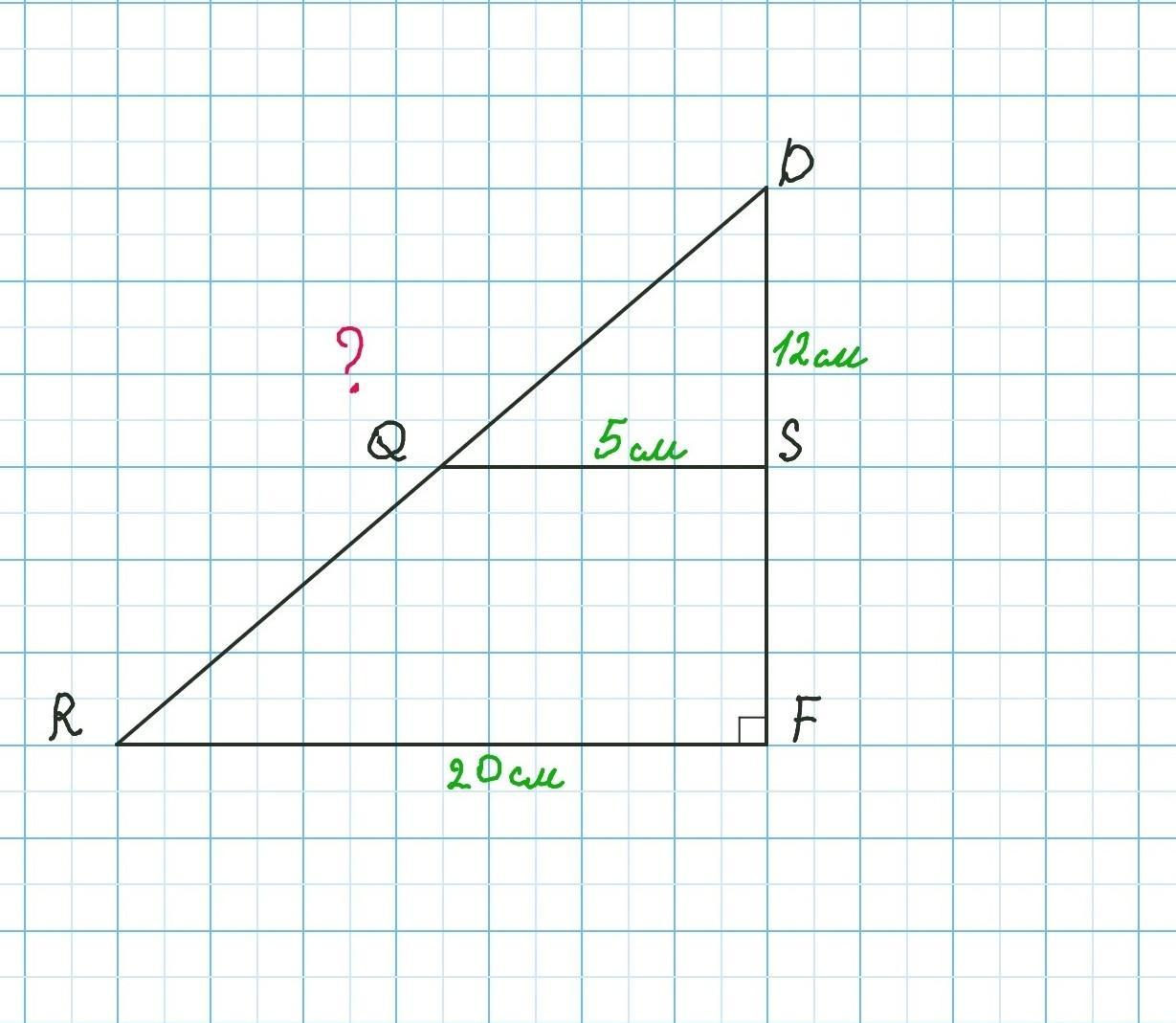
В треугольнике DFR DFR провели прямую, параллельную стороне FR FR так, что она пересекает стороны DF DF и DRDR в точках SS и QQ, соответственно.
Найди длину стороны DRDR , если площадь треугольника DSQ DSQ равна 3030 см^2
2
, SQ = 5 SQ=5 см, DS = 12 DS=12 см, FR =20 FR=20 см.
Вырази ответ в сантиметрах и запиши числом.
Ответы
Автор ответа:
3
Ответ:
DR=52см
Объяснение:
В треугольнике DFR провели прямую, параллельную стороне FR так, что она пересекает стороны DF и DR в точках S и Q, соответственно.Найди длину стороны DR , если площадь треугольника DSQ равна 30 см², SQ=5 см, DS=12 см, FR=20 см.
- Площадь треугольника равна половине произведения сторон на синус угла между ними.
1) S(DSQ)= ½×DS×SQ×sin∠DSQ. По условию: S(DSQ)=30см²
∠DSQ=90°. Следовательно треугольник DSQ прямоугольный. По теореме Пифагора найдём гипотезу QD:
см
2) Так как SQ II FR по условию, то ∠DSQ=∠DFR, как соответственные углы при параллельных прямых SQ и FR и секущей DF.
△DSQ подобен △DFR по двум углам (первый признак подобия треугольников): ∠DSQ=∠DFR, а ∠D-общий.
3)Найдём коэффициент подобия.
- Коэффициент подобия - это число k, равное отношению сходственных сторон подобных треугольников.
4) Найдём сторону DR:
см
DR = 52 см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: hjvfhecc
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: мамочка59
Предмет: Алгебра,
автор: lerika211
Предмет: Литература,
автор: SIMPL4E