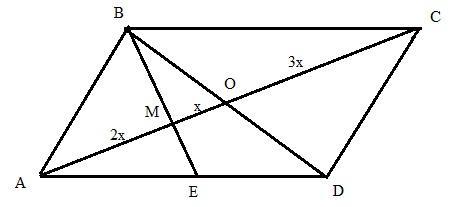
Помогите с решением пожалуйста

Ответы
Ответ:
Объяснение:
Проведём диагонали АС и BD, пересекающиеся в точке О.
Рассмотрим тр-к △ABD. У него АЕ=ED по условию, ВО=OD по свойству диагоналей параллелограмма. Значит ВЕ и АО - медианы этого треугольника, пересекающиеся в точке М.
Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1, считая от вершины треугольника.
Значит АМ:МО=2:1. При этом по свойству диагоналей АО=ОС, значит если х - 1 часть, то АМ=2х, МО=х, ОС=2х+х=3х, МС=3х+х=4х. Тогда АМ:МС=2х:4х=1:2.
Медиана треугольника делит его на два треугольника равной площади.
Значит медиана ВЕ делит тр-к △ABD на тр-ки S(ABE)=S(DBE). При этом по свойству диагоналей параллелограмма △ABD=△CDB => S(ABD)=S(CDB)=2*S(ABE);
S(BCDE)=S(CDB)+S(DBE)=2*S(ABE)+S(ABE)=3*S(ABE);
S(ABE)/S(BCDE)=S(ABE)/3*S(ABE)=1:3.