Question

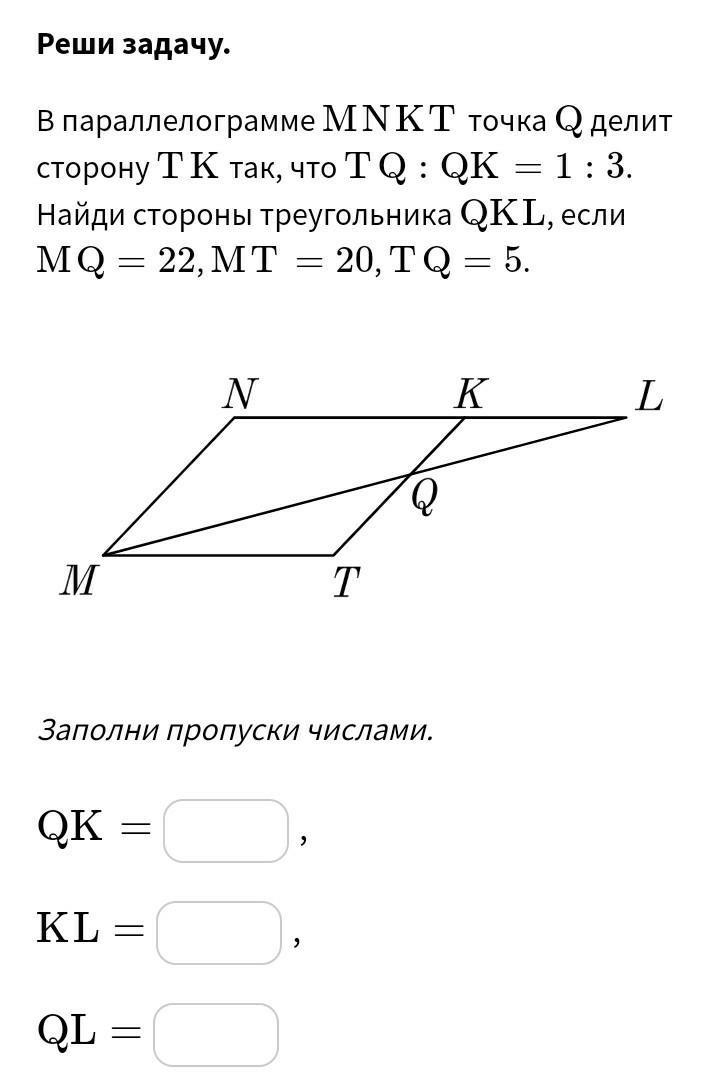
В параллелограмме  MNKT точка Q делит сторону TK так, что TQ:QK = 1:3. Найди стороны треугольника QKL, если MQ = 22, MT = 20, TQ =5.
срочно пожалуйста!!!​

Answer 1

Ответ:

QK = 15 см, KL= 60 см, QL= 66 см.

Объяснение:

1) Рассмотрим треугольники MQT и LQT.

Так как NL II MT, как стороны параллелограмма, то ∠NLM =∠TML, как внутренние накрест лежащие углы при параллельных прямых NL и MT и секущей ML.

∠KQL =∠TQM - как вертикальные.

△MQT подобен △LQT по двум углам (первый признак подобия треугольников).

2)Из подобия треугольников следует пропорциональность соответственных сторон:

$\dfrac{MQ}{QL} = \dfrac{TQ}{QK} = \dfrac{MT}{KL} = k$

где k - коэффициент подобия.

$k = \dfrac{TQ}{QK} = \dfrac{1}{3}$

Тогда стороны треугольника QKL будут равны:

$\dfrac{MQ}{QL} = \dfrac{1}{3} , \: \: QL = 3 \times MQ = 3\times 22 = 66 \\ \\ \dfrac{MT}{KL} = \dfrac{1}{3} , \: \: KL = 3 \times MT = 3\times 20 = 60 \\ \\ \dfrac{TG}{QK} = \dfrac{1}{3} , \: \: QK = 3 \times TG = 3\times 5 = 15$

Стороны треугольника QKL: QK = 15 см, KL= 60 см, QL= 66 см.