Предмет: Алгебра,
автор: termew
18 вариант 3-4 задание решите пожалуйста
Приложения:
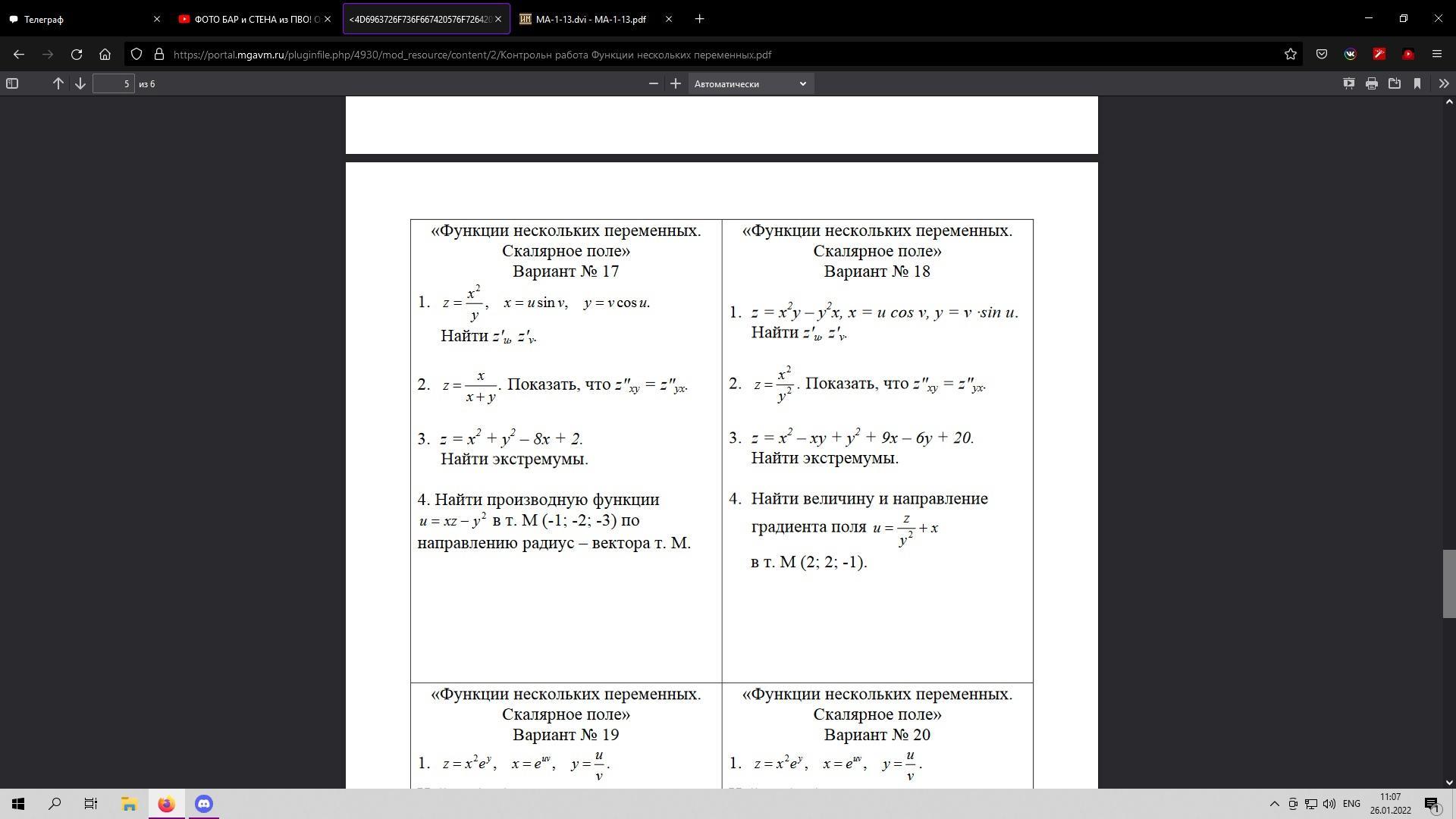
Ответы
Автор ответа:
1
Ответ:
Необходимые условия .
Критическая точка .
Проверим достаточные условия.
функция имеет экстремум и так как А>0 , то это минимум .
Вычислим значение минимума функции.
Похожие вопросы
Предмет: Русский язык,
автор: гуз41
Предмет: Русский язык,
автор: bukvaruk
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: il4ik81
Предмет: Алгебра,
автор: 2303091096