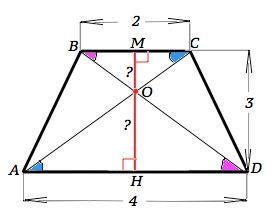
Основания трапеции равны 2 см и 4 см, а высота -
3 см. Найди расстояния от точки пересечения
диагоналей трапеции к её основаниям.
Длины укажи в порядке возрастания.
Ответ:
см,
см.
Ответы
Ответ: 1 см; 2 см.
Объяснение ( подробно): Сделаем рисунок, соответствующий условию.
Треугольники, образованные основаниями и диагоналями трапеции, подобны по двум углам (накрестлежащими при пересечении параллельных ВС и АD диагоналями).
Коэффициент подобия AD:BC=4:2, т.е. k=2
Расстоянием от точки до прямой является длина отрезка, проведенного между ними перпендикулярно. Пусть О - точка пересечения диагоналей. Тогда ОМ и ОН - высоты подобных треугольников ВОС и АОD и являются частями высоты трапеции МН.
Примем одну часть отношения расстояния от точки пересечения диагоналей трапеции к её основаниям равной х.
Отношение сходственных элементов подобных треугольников равно их коэффициенту подобия. =>
ОН:МО=2:1; МН=3=2х+х=3х => х=3:3=1,
МО=1 см; ОН=2 см.