Question

второй и третий признак подобия треугольников​

Answer 1

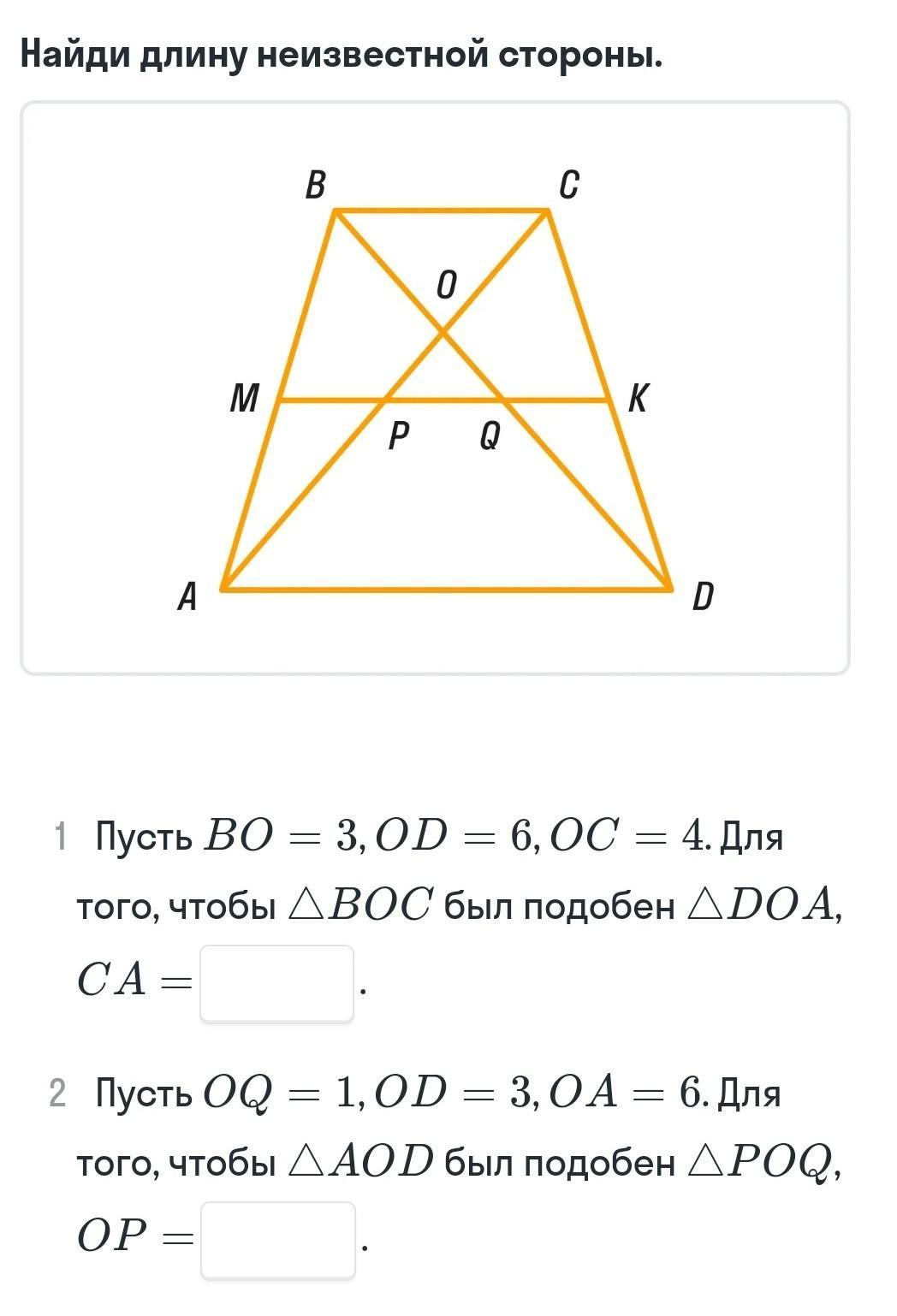
1. Для того, чтобы ΔBOC был подобен ΔDOA, надо, чтобы $\displaystyle \frac{BO}{OD}=\frac{CO}{OA}$ и ∠BOC=∠AOD.

Действительно, ∠BOC=∠AOD, т.к. они вертикальные.

$\displaystyle OA=\frac{OD \cdot CO}{BO} =\frac{6 \cdot 4}{3} =8\\ CA=OA+CO=8+4=12$

Ответ: CA=12.

2. Чтобы ΔAOD был подобен ΔPOQ, надо, чтобы $\displaystyle \frac{OP}{PA} = \frac{OQ}{QD}$ (∠POQ у них общий).

$\displaystyle \frac{OP}{PA} = \frac{OQ}{QD} = \frac{OQ}{OD-OQ} = \frac{1}{3-1} =\frac{1}{2}$

Пусть OP=x, PA=2x, тогда OP+PA=x+2x=OA=6

x+2x=6

3x=6

x=OP=2

PA=2x=2·2=4.

Ответ: OP=2.