Предмет: Алгебра,
автор: girlokay
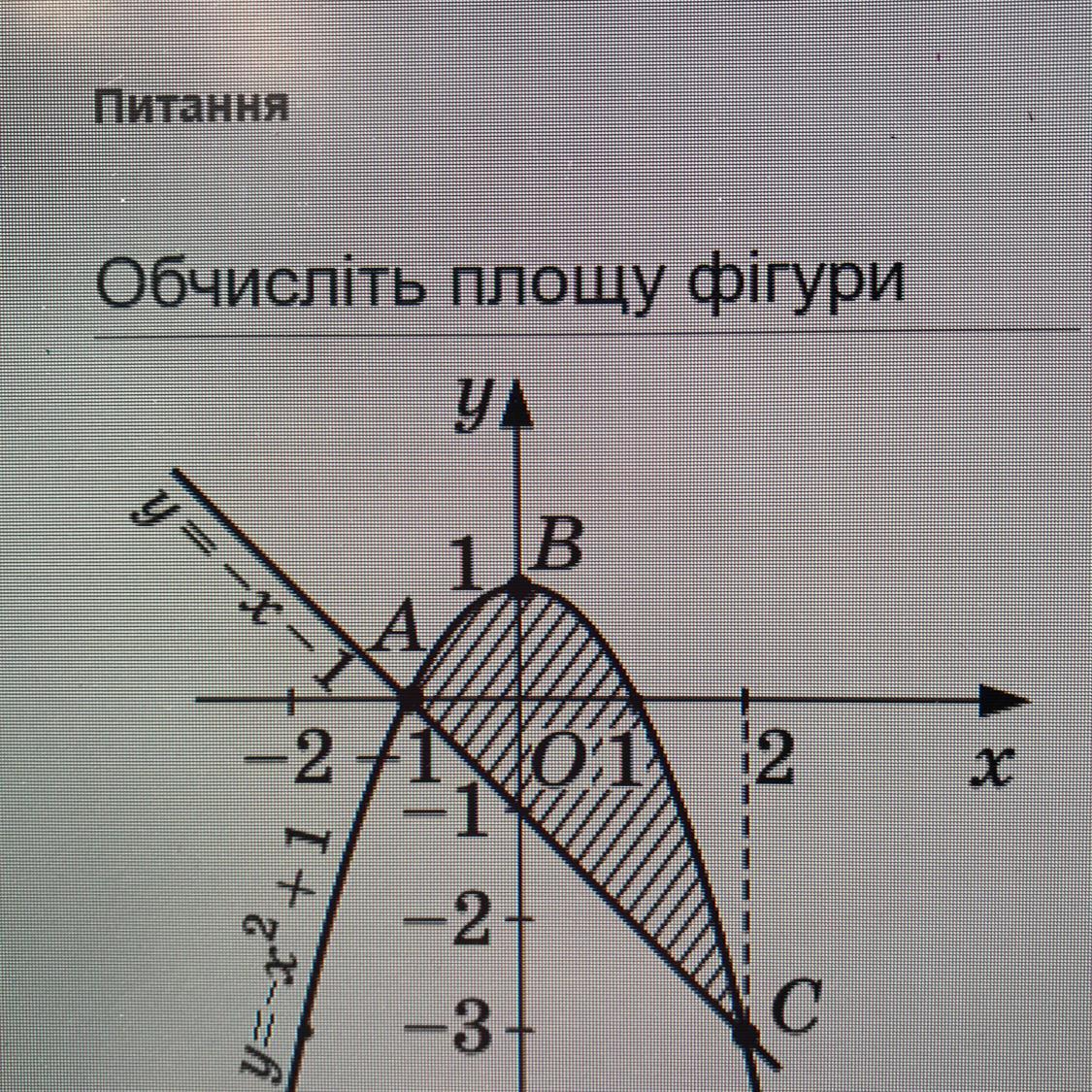
Найти площадь ещё одной фигуры
Приложения:
Ответы
Автор ответа:
1
filuksistersp735lh:
там в второй строчке ответа должно быть 2×2 потому что в интеграле +2 и так же в конце первой строчки должно быть не х а 2х
Автор ответа:
1
Ответ:
21/2
Объяснение:
Площадь считаем по формуле Ньютона-Лейбница,
пределы интегрирования х₁ = -1; х₂ = 2
функции у₁ = х² +1; у₂ = -х -1
Похожие вопросы
Предмет: Русский язык,
автор: korobkinan476
Предмет: Окружающий мир,
автор: kjlj45454
Предмет: Русский язык,
автор: Gorbunova80
Предмет: Русский язык,
автор: Аноним
Предмет: Геометрия,
автор: yulia72532