Question

алгебра 11 класс
:(...​

Answer 1

Ответ:

Пошаговое объяснение:

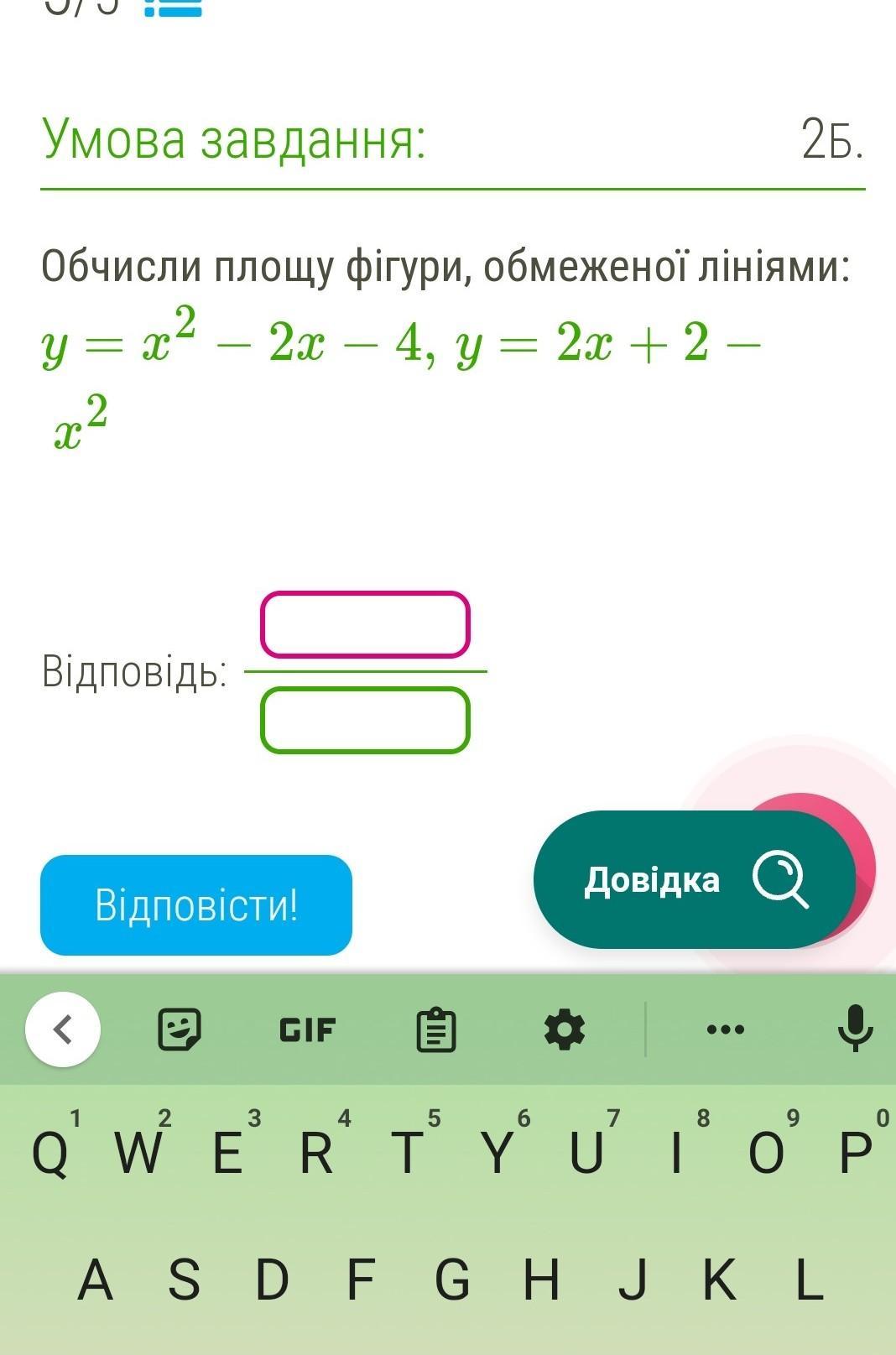
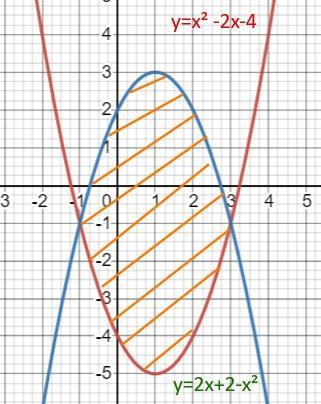
Рисуем графики, получаем фигуру, пределы интегрирования и подынтегральное выражение

Пределы интегрирования х₁ = -1;  х₂ = 3

функции у₁ = 2х+2 -х²;    у₂ = х² -2х -4

подынтегральное выражение 2х+2 -х² -(х² -2х -4 )=$\displaystyle S=\int\limits^3_ {-1} {( -2x^2 +4x + 6 ) }\, dx =-2\frac{x^3}{3} \bigg|_{-1}^3+4\frac{x^2}{2} \bigg|_{-1}^3+6x\bigg|_{-1}^3=-\frac{56}3} +16+24=\boldsymbol {\frac{64}{3} }$

Теперь мы можем посчитать площадь фигуры по формуле Ньютона-Лейбница.

Можно было и разбить фигуру на две по линии у = -1, но результат суммы площадей выйдет тот же, что и у нас.