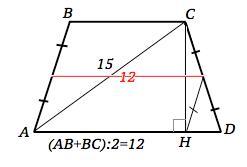
стредняя линия равнобедренной трапеции равна 12 см диагональ 15см. найдите площадь трапеции.
Ответы
Ответ:
АВСД равнобедренная трапеция
ВД=15см ср.линия=12см
проведем высоты ВН и СК
ΔАНВ=ΔДКС т.к АВ=СД ВН=СК поэтому АН=КД
ср.линия =(АД+ВС)/2=12см
АД+ВС=24см
АД+ВС=2КД+2ВС
КД+ВС=НК+КД=НД=12см
ΔВНД прямоугольный
ВН²=ВД²-НД²=225-144=81
ВН=9см
S=(АД+ВС)/2*ВН=12*9=108см²
Объяснение:
Вариант решения.
Ответ: 108 см²
Объяснение:
Средняя линия трапеции равна полусумме оснований – в трапеции АВСД сумма оснований равна 2•12=24 см.
Проведем диагональ АС и высоту СН.
В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит основание на отрезки, больший из которых равен полусумме, а меньший - полуразности оснований.
Поэтому АН=(ВС+АД):2=12 см.
Треугольник АСН - прямоугольный. По т.Пифагора СН=√(АС^2-АН^2)=9 см.
Площадь трапеции равна произведению высоты на полусумму оснований.
Ѕ (ABCD)=9•12=108 см²