Предмет: Алгебра,
автор: maksimmiller91
Алгебра 9 класс. 30 БАЛЛОВ
Докажите неравенство
Приложения:
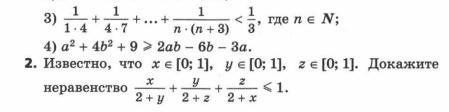
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Объяснение:
Выполним запись:
Тогда верно, что:
Значит неравенство можно переписать:
Верность этого неравенства очевидна для любого , а значит и исходное неравенство верно.
Доказано!
dfgddffxx:
здравствуйте помогите пожалуйста решить задачу
Похожие вопросы
Предмет: Русский язык,
автор: Basilica2006
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: егор776
Предмет: Физика,
автор: uronlion
Предмет: Английский язык,
автор: popi26