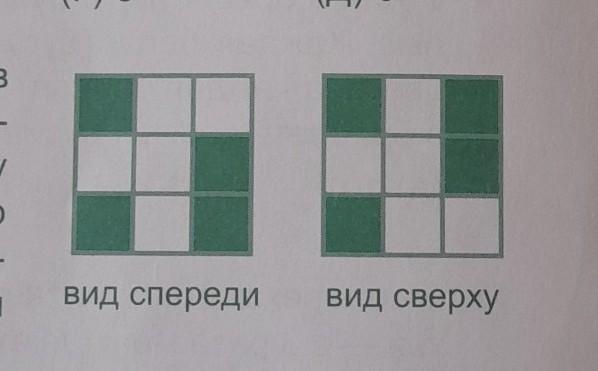
Из закрашенных и прозрачных кубиков Смартик хочет сложить куб 3х3х3 та- кой, чтобы вид спереди и вид сверху этого куба были как на рисунке. Сколько разных значений может принимать ко- личество закрашенных кубиков в таком кубе? (А) 1 (6) 2 (В) (Г) 4 (Д) 5
Ответы
Ответ: (Д) 5.
Складываем куб из закрашенных и прозрачных кубиков по три на каждое ребро. Чтобы вид спереди и вид сверху на куб соответствовали условию задачи, количество закрашенных кубиков может быть равным 4, 5, 6, 7 или 8, то есть всего 5 разных значений.
Объяснение:
Складываем куб из закрашенных и прозрачных кубиков по три на каждое ребро.
3×3×3 = 27
Значит, понадобится 27 маленьких кубиков.
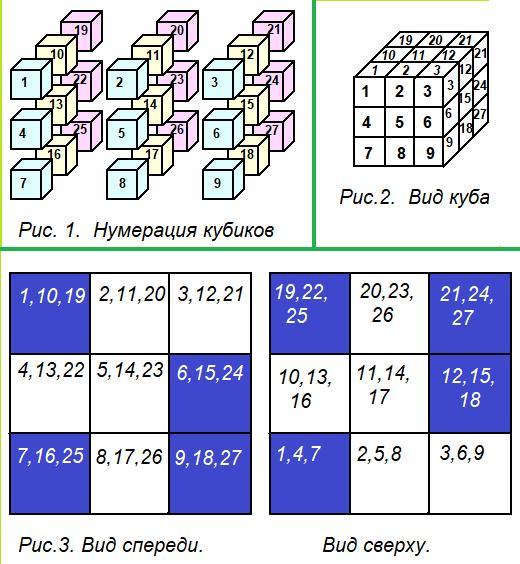
Пронумеруем кубики (рис. 1). Куб с нумерованными кубиками выглядит, как на рисунке 2.
По условию задачи посмотрим на куб спереди (рис.3).
Ряды кубиков, которые расположены за кубиками с номерами 2, 3, 4, 5 и 8 на рисунке остались прозрачными, значит, ни один кубик в этих рядах не может быть закрашенным.
За кубиком с номером 2 будут находиться кубики с номерами 11 и 20.
За кубиком с номером 3 будут находиться кубики с номерами 12 и 21.
За кубиком с номером 4 будут находиться кубики с номерами 13 и 22.
За кубиком с номером 5 будут находиться кубики с номерами 14 и 23.
За кубиком с номером 8 будут находиться кубики с номерами 17 и 26.
Все эти 15 кубиков не могут быть закрашенными.
Теперь по условию задачи посмотрим на куб сверху (рис.3).
Столбики кубиков, которые расположены под кубиками с номерами 2, 3, 10, 11 и 20 на рисунке остались прозрачными, значит, ни один кубик в этих столбиках не может быть закрашенным.
Под кубиком с номером 2 будут кубики с номерами 5 и 8.
Под кубиком с номером 3 будут кубики с номерами 6 и 9.
Под кубиком с номером 10 будут кубики с номерами 13 и 16.
Под кубиком с номером 11 будут кубики с номерами 14 и 17.
Под кубиком с номером 20 будут кубики с номерами 23 и 26.
Все эти 15 кубиков не могут быть закрашенными.
Посчитаем, сколько всего осталось кубиков, которые могут быть закрашенными:
номера 1, 7, 15, 18, 19, 24, 25, 27 - всего 8 кубиков. Это наибольшее значение для количества закрашенных кубиков. В каждом ряду и в каждом столбце на видах спереди и сверху есть по два закрашенных кубика, какие-то из них можно будет убрать.
Так как вид спереди и вид сверху содержат по 4 закрашенных клетки, то количество закрашенных кубиков не может быть меньше, чем 4.
Будем по одному заменять закрашенные кубики незакрашенными и проверять, соответствует ли куб видам спереди и сверху.
Примеры закрашенных кубиков:
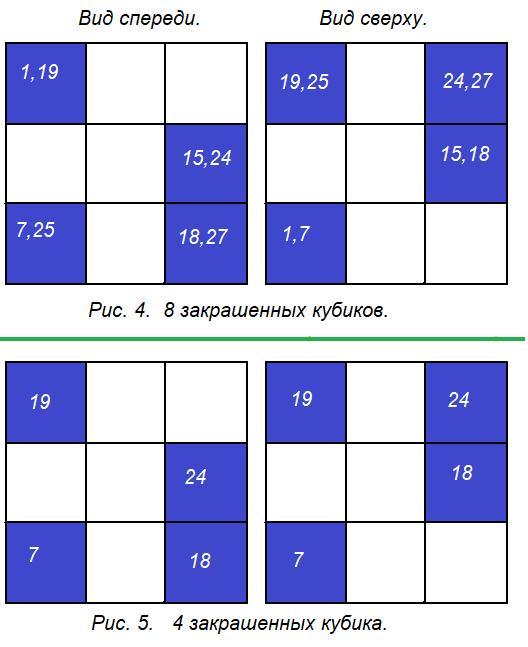
1) 1, 7, 15, 18, 19, 24, 25, 27 - всего 8 кубиков. (Рис.4.)
2) 7, 15, 18, 19, 24, 25, 27 - всего 7 кубиков.
3) 7, 18, 19, 24, 25, 27 - всего 6 кубиков.
4) 7, 18, 19, 24, 25 - всего 5 кубиков.
5) 7, 18, 19, 24 - всего 4 кубика. (Рис.5.)
Количество закрашенных кубиков может быть равным 4, 5, 6, 7 или 8, то есть всего 5 разных значений.
Ответ: (Д) 5.