Question

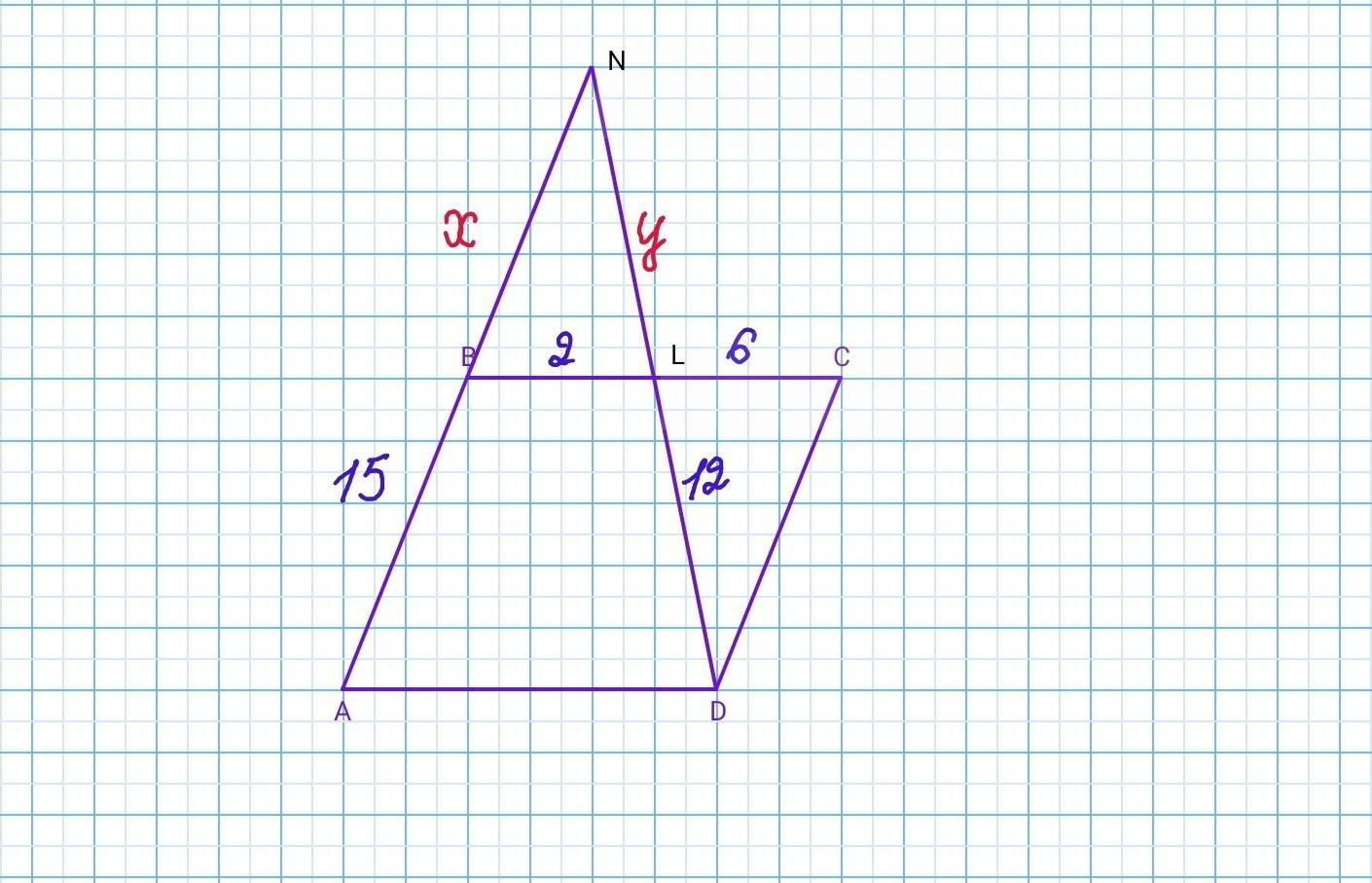
На стороне BC параллелограмма ABCD
отмечена точка L. Прямая DL пересекает прямую AB в точке N. Известно, что AB = 15, BL = 2, DL = 12, CL = 6.
Найдите длины LN и BN
Срочно помогите(

Answer 1

Ответ:

LN = 4 ед

BN = 5 ед

Объяснение:

у параллелограмма противоположные стороны попарно параллельны и равны.

Поэтому ВС ІІ AD. AD=BC=BL+CL=2+6=8 ед.

Рассмотрим треугольники AND и BNL.

∠N - общий, ∠NAD=∠NBL, как соответственные углы при параллельных прямых BC и AD и секущей AN.

△AND подобен △BNL по двум углам (первый признак подобия треугольников)

Из подобия треугольников следует пропорциональность соответственных сторон:

$\dfrac{AN}{BN} = \dfrac{ND}{NL} = \dfrac{AD}{BL}$

Пусть BN = x, NL = y. AN = 15+x, ND = 12+y.

$\dfrac{15 + x}{x} = \dfrac{12 + y}{y} = \dfrac{8}{2} \\ \\ \dfrac{15 + x}{x} = \dfrac{8}{2} \: \: \: \: \: \: \: \: \: \: \dfrac{12 + y}{y} = \dfrac{8}{2} \\ \\ 4x = 15 + x \: \: \: \: \: \: \: \: \: \: 4y = 12 + y \\ \\ 3x = 15 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: 3y = 12 \\ \\ x = 5 \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \:y = 4$

BN = 5ед, NL=4 ед