Question

100 БАЛЛОВ СРОЧНО
Задача с решением

Answer 1

Ответ:

DE = 48/√73 ≈ 5,62 ед.

Объяснение:

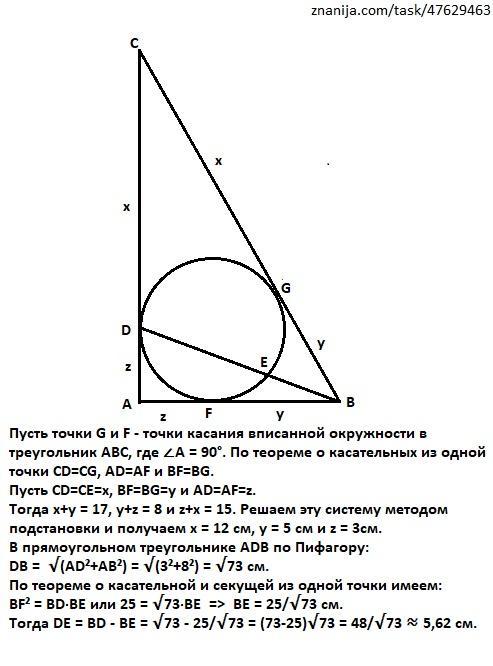
Пусть точки G и F - точки касания вписанной окружности в треугольник АВС, где ∠А = 90°. По теореме о касательных из одной точки CD=CG, AD=AF и BF=BG.

Пусть CD=CE=x, BF=BG=y и AD=AF=z.

Тогда x+y = 17, y+z = 8 и z+x = 15. Решаем эту систему методом подстановки и получаем x = 12 cм, y = 5 см и z = 3см.

В прямоугольном треугольнике ADB по Пифагору:

DB =  √(AD²+AB²) = √(3²+8²) = √73 см.

По теореме о касательной и секущей из одной точки имеем:

BF² = BD·BE или 25 = √73·BE  =>  ВЕ = 25/√73 см.

Тогда DE=BD - BE =√73 - 25/√73 =(73-25)√73 =48/√73 ≈ 5,62 см.