Помогите пожалуйста. Найти наименьшее и наибольшее значения функции y=f(x) на заданном отрезке [a;b]:
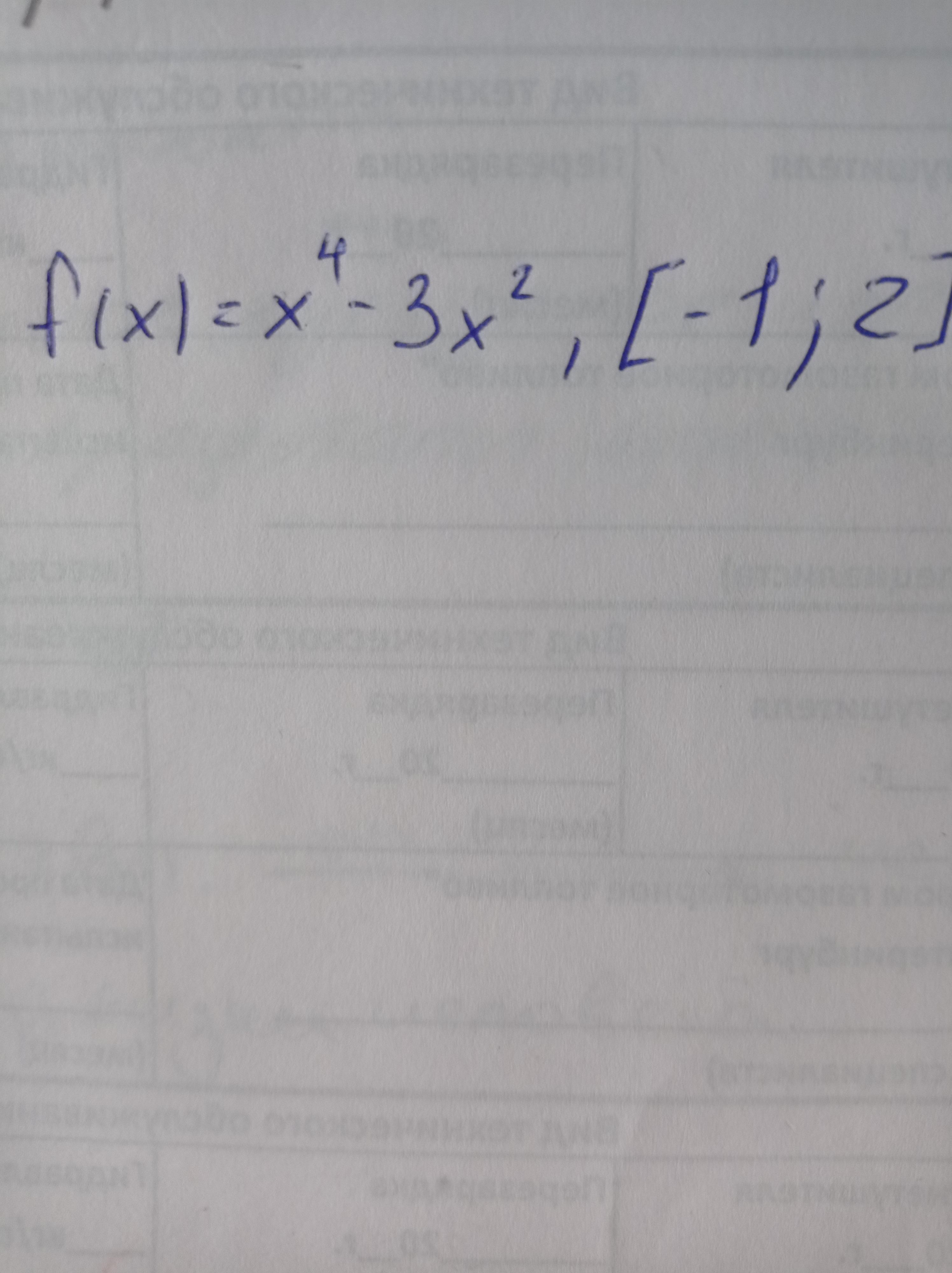
Ответы
Ответ:
f(x)=x^4 - 3x^2
найдем производную данной функции:
f*(x)=4x^3 - 6x
приравняем производную к нулю и найдем корни, получившегося уравнения:
4х^3 - 6х =0
2х*(2х^2 - 3) =0
4x*(x^2 - 1.5)=0
x*(x - (корень из 1,5))(х + (корень из 1,5)) = 0
корень из (-1,5) получается меньше (-1), значит не входит в заданный отрезок.
у нас получается прямая:
------(0)-----------(корень из 1,5)-----------
на этой прямой начиная справа расставляем знаки плюса и минуса:
-------(0)------------(корень из 1,5)-----------
+ - +
получается на интервале, где стоит знак + производная больше нуля, значит функция возрастает, а где - производная меньше нуля и функция убывает.
можно себе в тетради ставить стрелочки вверх, где + и вниз, где -.
в общем то точки экстремумов:
в точке 0 функция принимает максимальное значение, а в точке (корень из 1,5) - минимальное.
теперь подставь эти значения вместо х и посчитай)
получившиеся результаты и будут наибольшим и наименьшим значением функции.