Предмет: Алгебра,
автор: temirovbahrom3p7s6ng
Помогите пожалуйста разобраться!!!! Желательно все 3 примера кто как сможет, заранее благодарен
Приложения:
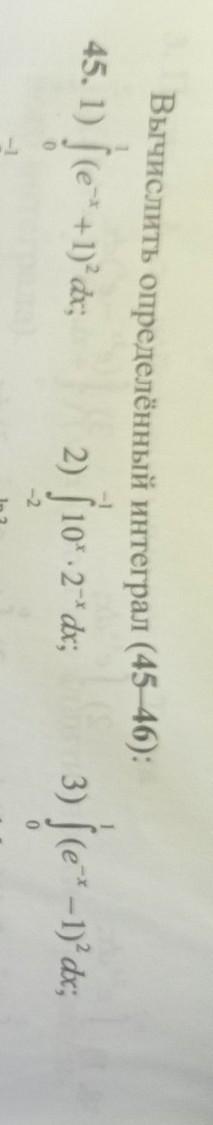
Ответы
Автор ответа:
1
Ответ:
Формула Ньютона-Лейбница
Похожие вопросы
Предмет: Английский язык,
автор: лиза1517
Предмет: Русский язык,
автор: PauTinKaYT
Предмет: Қазақ тiлi,
автор: Alisavin99
Предмет: Математика,
автор: sypatai
Предмет: История,
автор: umideleven