Question

из точки к прямой проведены две наклонные. длина одной из них равна 10см, а её проекции 6 см. Найдите длину второй наклонной, если она образует с прямой угол 30°​

Answer 1

Ответ:

36

Не факт.............................

Ну....

Answer 2

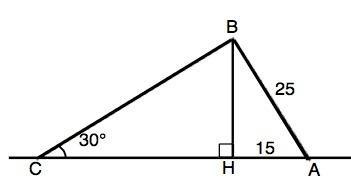
Ответ:Расстояние от данной точки В до прямой равно длине проведенного к ней перпендикуляра ВН. Отрезок ВН - перпендикулярен прямой и является катетом треугольников, в которых наклонные – гипотенузы.

Из ∆АВН по т.Пифагора

ВН=√(ВА²-АН²)=√625-225)=20 см.

Из ∆ВСН: Катет ВН противолежит углу 30°. Синус 30°=1/2

Поэтому наклонная ВС=BH:sin30°=20:(1/2)=40 см

-------

Можно просто вспомнить, что в прямоугольном треугольнике длина гипотенузы в два раза больше катета, лежащего против угла 30°⇒ ВС=2•20=40 см

Пошаговое объяснение: