Question

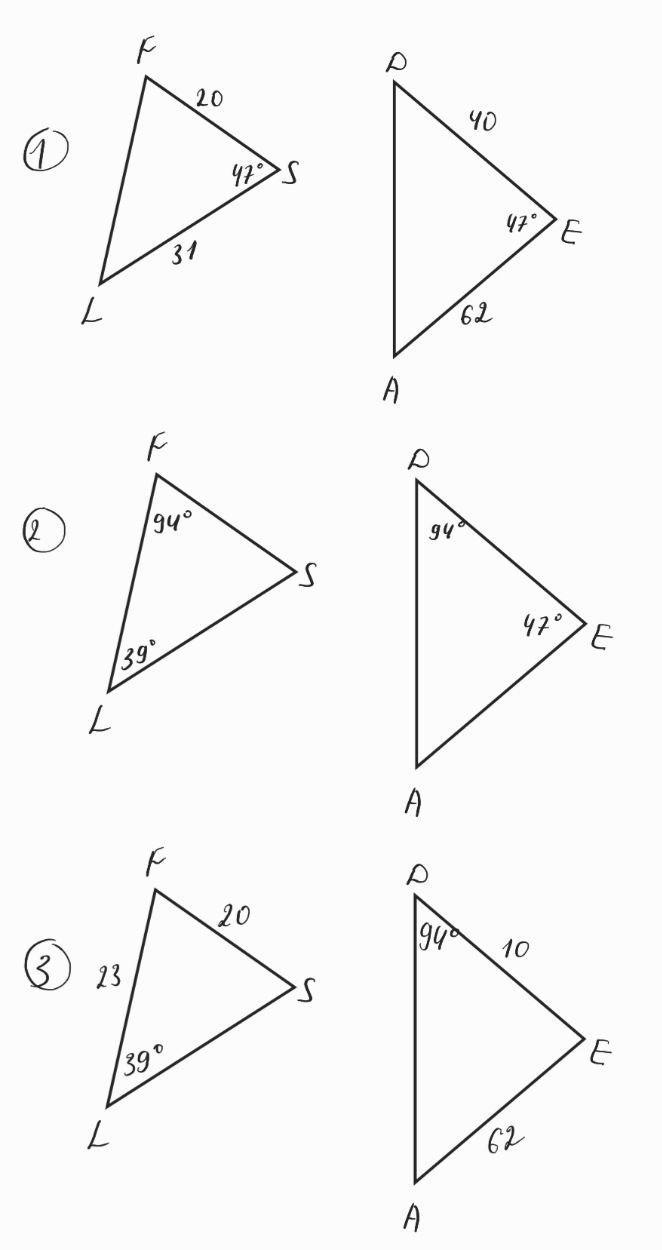
Известны некоторые величины треугольников LFS и ADE . Определи, подобны эти треугольники или нет в каждом из случаев.

Answer 1

1)

∠S = ∠E (по условию).

$\frac{FS}{DE}=\frac{20}{40}=\frac{1}{2}$.

$\frac{LS}{AE} =\frac{31}{62} =\frac{1}{2}$.

Значит, $\frac{FS}{DE}=\frac{LS}{AE}$.

△LFS ~ △ADE по 2-ому признаку (двум сторонам и углу).

Ответ: треугольники подобны.

2)

∠F = ∠D (по условию).

По теореме о сумме углов треугольника:

∠F + ∠L + ∠S = 180°.

Отсюда, ∠S = 180 - (94 + 39) = 47° = ∠E.

△LFS ~ △ADE по 1-ому признаку (двум углам).

Ответ: треугольники подобны.

3)

$\frac{FS}{DE}=\frac{20}{10}=2$.

Если данные треугольники подобны, то и сторона LS должна быть больше стороны AE в 2 раза, то есть должна равняться 124.

Это невозможно, потому что, в таком случае, LS > FS + FL, а сторона треугольника должна быть меньше суммы двух других.

Ответ: треугольники не подобны.