Предмет: Математика,
автор: aksenovasvetaaaaaaa7
Исследовать ряд на сходимость.
Приложения:
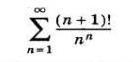
Ответы
Автор ответа:
1
Ответ: ряд сходится.
Пошаговое объяснение:
Запишем выражение для n+1 - го члена ряда: aₙ₊₁=(n+2)!/[(n+1)^(n+1)]=(n+1)!*(n+2)/[(n+1)^(n+1)] и составим отношение n-1 - го члена к n-му: aₙ₊₁/aₙ=(n^n)*(n+2)/[(n+1)*(n+1)^n]. Надём предел этого выражения: lim aₙ₊₁/aₙ=lim (n+2)/(n+1)*lim (n^n)/[(n+1)^n]. Но lim (n+2)/(n+1)=1, а для нахождения предела выражения (n^n)/[(n+1)^n] сначала представим его в виде (n^n)/[(n+1)^n]=[1-1/(n+1)]^n. Положим -1/(n+1)=m, тогда n=-1/m-1 и при n⇒∞ m⇒0. Тогда данное выражение примет вид: (1+m)^(-1/m-1)=1/[(1+m)^1/m)]*1/(1+m). Его предел равен 1/lim[(1+m)^1/m)]*1/lim(1+m)=1/e*1=1/e. Отсюда lim aₙ₊₁/aₙ=1*1/e<1, поэтому по признаку Даламбера ряд сходится.
Похожие вопросы
Предмет: Английский язык,
автор: dashaa8
Предмет: Русский язык,
автор: dashkapomojet
Предмет: Английский язык,
автор: великий5
Предмет: Литература,
автор: Alinok54
Предмет: Литература,
автор: artur13valiev