Предмет: Математика,
автор: HEKUCTOH
Решить два примера. Photomath не помог
Приложения:


DNHelper:
а во втором что нужно сделать?
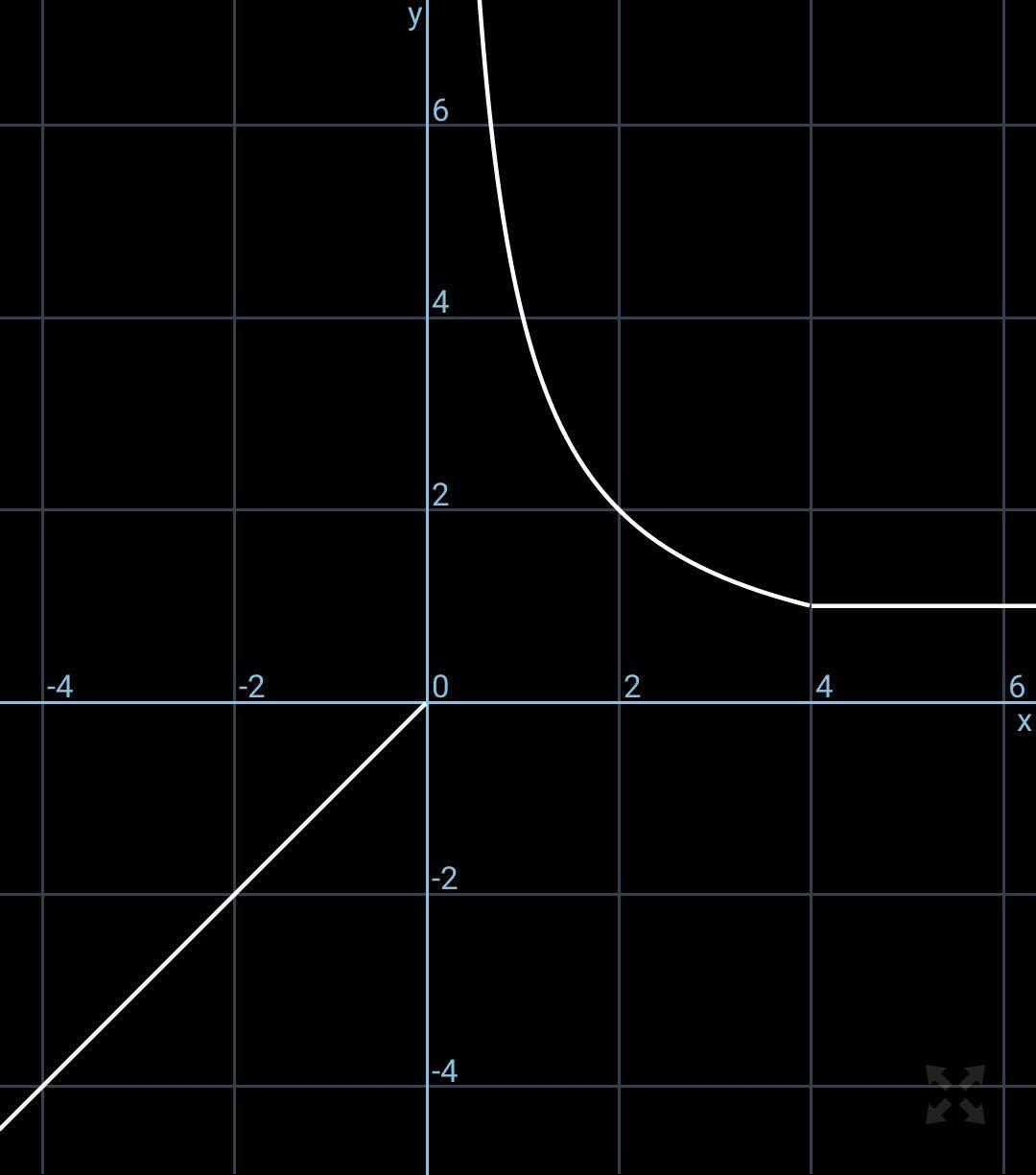
Найти точки разрыва функции, если они существуют. Сделать чертеж функции.
Ответы
Автор ответа:
1
Ответ:
1.
2. x = 0
Пошаговое объяснение:
1.
2. Потенциальные точки разрыва: x = 0 и x = 4. Рассмотрим односторонние пределы в этих точках.
В точке x = 0:
Это разрыв второго рода.
В точке x = 4:
Поскольку f(4) = 1 и односторонние пределы равны значению функции в этой точке, функция на данном промежутке непрерывна.
Приложения:
Спасибо
Похожие вопросы
Предмет: Русский язык,
автор: 3класс30
Предмет: Другие предметы,
автор: Madina140316
Предмет: Русский язык,
автор: МашкаАстратова
Предмет: Французский язык,
автор: AminaRo555
Предмет: Математика,
автор: annadmitrievnaaaa