Предмет: Алгебра,
автор: mansurtatygulov
помогите пж нужно срочно
Приложения:
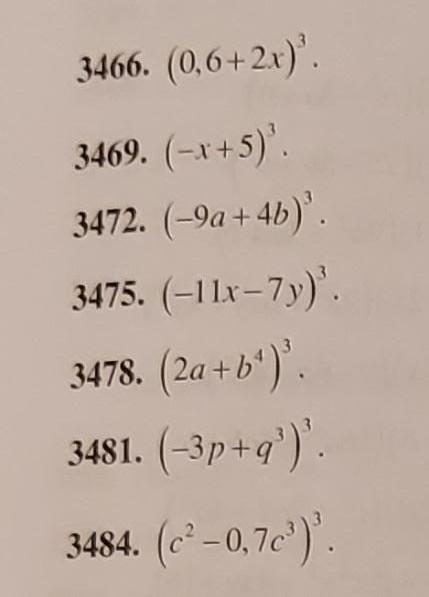
Ответы
Автор ответа:
1
Решение
Формулы
mansurtatygulov:
не доконса же зделано
в плане?
Автор ответа:
0
Ответ:
1)(0,6+2x)3=(53+2x)3=12527+2554x+536x2+8x3.2)(−x+5)3=(5−x)3=125−75x+15x2−x3=−x3+15x2−75x+125.3)(−9a+4b)3=(4b−9a)3=64b4−432ab2+972a2b−729a3.4)(−11x−7y)3=(−11x)3−3∗(−11x)2∗7y+3∗(−11)x∗(7y)2−(7y)3=−1331x3−3∗121x2∗7y+3∗(−11)x∗49y2−343y3=−1331x3−2541x2y−1617xy2−343y3.5)(2a+b4)3=8a3+3∗4a2b4+3∗2ab8+b12=8a3+12a2b4+6ab8+b12.6)(−3p+q3)3=(q3−3p)3=q9−9pq6+27p2q3−27p3.
7) (c^2-0,7c^3)^3=c^6-2,1c^7+1,47c^8-0,343c^9.7)(c2−0,7c3)3=c6−2,1c7+1,47c8−0,343c9.
Формулы
\begin{gathered}(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3.\\ (a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3.\end{gathered}(a+b)3=a3+3a2b+3ab2+b3.(a−b)3=a3−3a2b+3ab2−b3.
a+b)3=a3+3a2b+3ab2+b3.(a−b)3=a3−3a2b+3ab2−b3.
прости пж случайно скопировалочь не то
Похожие вопросы
Предмет: Английский язык,
автор: Lala2006
Предмет: Русский язык,
автор: oksanabogomolova
Предмет: Русский язык,
автор: дашенька113
Предмет: Английский язык,
автор: nekit104535
Предмет: Математика,
автор: Mirolslava102007