Предмет: Геометрия,
автор: ripepineapple1833
срочнооии
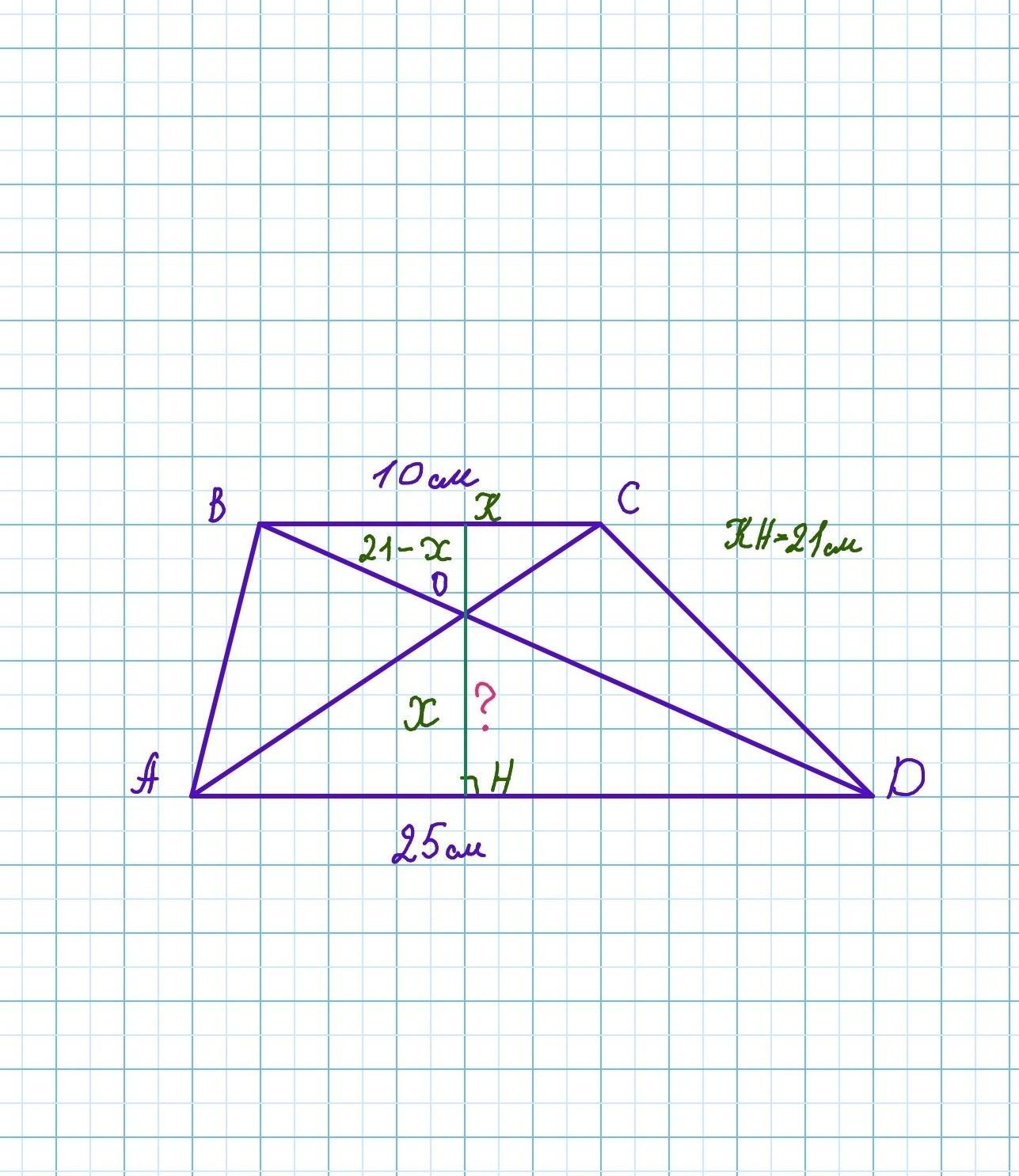
В трапеции основания равны 10 см и 25 см, а высота 21 см. Чему равно расстояние от точки пересечения диагоналей трапеции до ее большего основания?
Ответы
Автор ответа:
4
Ответ:
15 см
Объяснение:
Так как основания трапеции параллельны, а диагонали трапеции являются секущими, то ∠CBD =∠ADB, ∠BCA = ∠DAC - как внутренние накрест лежащие углы при параллельных прямых ВС и AD и секущих BD и AC.
Следовательно △ВОС подобен △ DOA по двум углам (первый признак подобия треугольников).
Коэффициент подобия этих треугольников равен отношению оснований трапеции:
Отношение длин соответствующих элементов подобных треугольников равно коэффициенту подобия. Пусть высота большего треугольника равна х см, тогда высота меньшего треугольника равна (21 - х) см.
Тогда
х=15 см
Расстояние от точки пересечения диагоналей трапеции до ее большего основания равно 15 см
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: xant010
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: ksks17
Предмет: Алгебра,
автор: pospelov89ru
Предмет: Русский язык,
автор: kurbanbegimzhan