Question

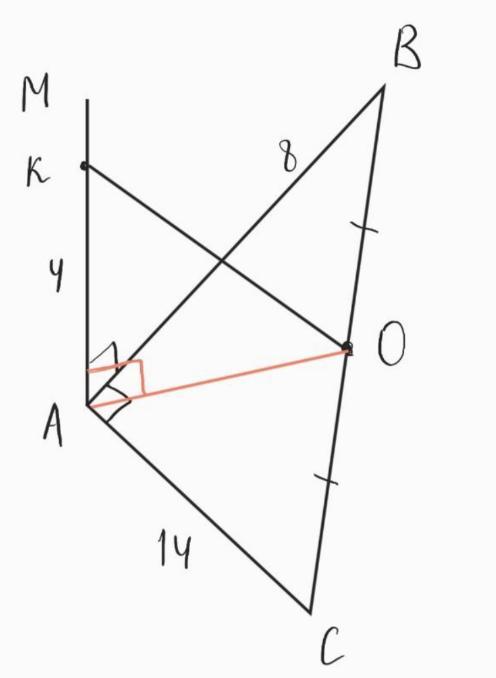
Катеты прямоугольного треугольника АВ = 8 см и АС = 14 см перпендикулярны прямой АМ, на которой отмечена точка К, так что АК = 4 см. Найдите расстояние от точки К до середины гипотенузы​

Answer 1

Найдем BC - гипотенузу прямоугольного треугольника ABC, используя теорему Пифагора:

$BC = \sqrt{AB^2 + AC^2} = \sqrt{8^2 + 14^2 } = \sqrt{64+196}=\sqrt{260}=2\sqrt{65}$.

Проведем АО — медиану △ ABC.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, поэтому:

$AO = \frac{BC}{2}=\frac{2\sqrt{65} }{2}=\sqrt{65}$.

Прямая AM перпендикулярна пересекающимся прямым АВ и АС. Это значит, что АМ ⊥ (ABC).

Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей на ней.

Отсюда, AM ⊥ AO и потому △ АКО является прямоугольным.

Найдем КО - расстояние от точки К до середины гипотенузы, используя теорему Пифагора:

$KO = \sqrt{4^2 + (\sqrt{65})^2 } = \sqrt{16 + 65}=\sqrt{81} =9$.

Ответ: 9.