Предмет: Алгебра,
автор: ata221
СРОЧНО!!! Решите иррациональные неравенства (на фото)
11 класс. Тема: "Иррациональные неравенства" (применять основные равносильные соотношения... (9))
Приложения:
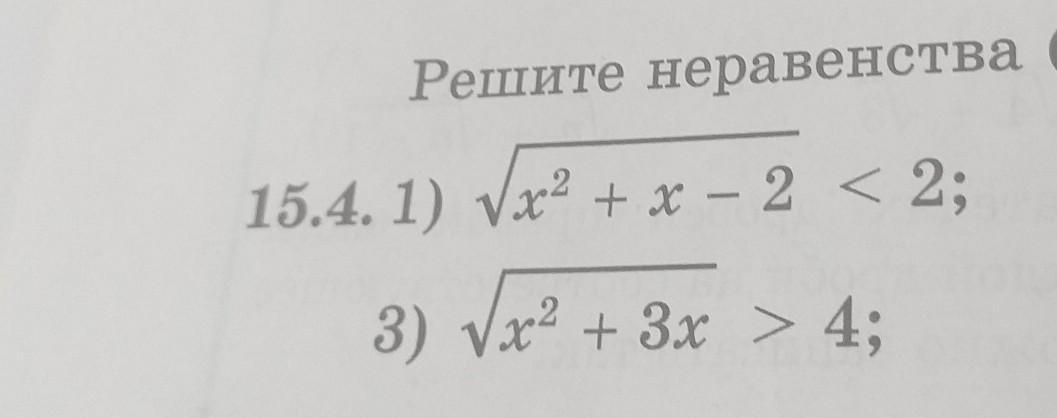
Ответы
Автор ответа:
0
Ответ:
P.S. Можно не записывать ОДЗ: , так как при возведении в квадрат обеих частей неравенства мы записали более строгое неравенство:
, и условия ОДЗ выполняются тем более .
Похожие вопросы
Предмет: Українська мова,
автор: zhenyaeerdd
Предмет: Английский язык,
автор: kerelaeva17
Предмет: Окружающий мир,
автор: хеди16
Предмет: Алгебра,
автор: zhenyayatskovp9cgzu
Предмет: Алгебра,
автор: vika5780