Question

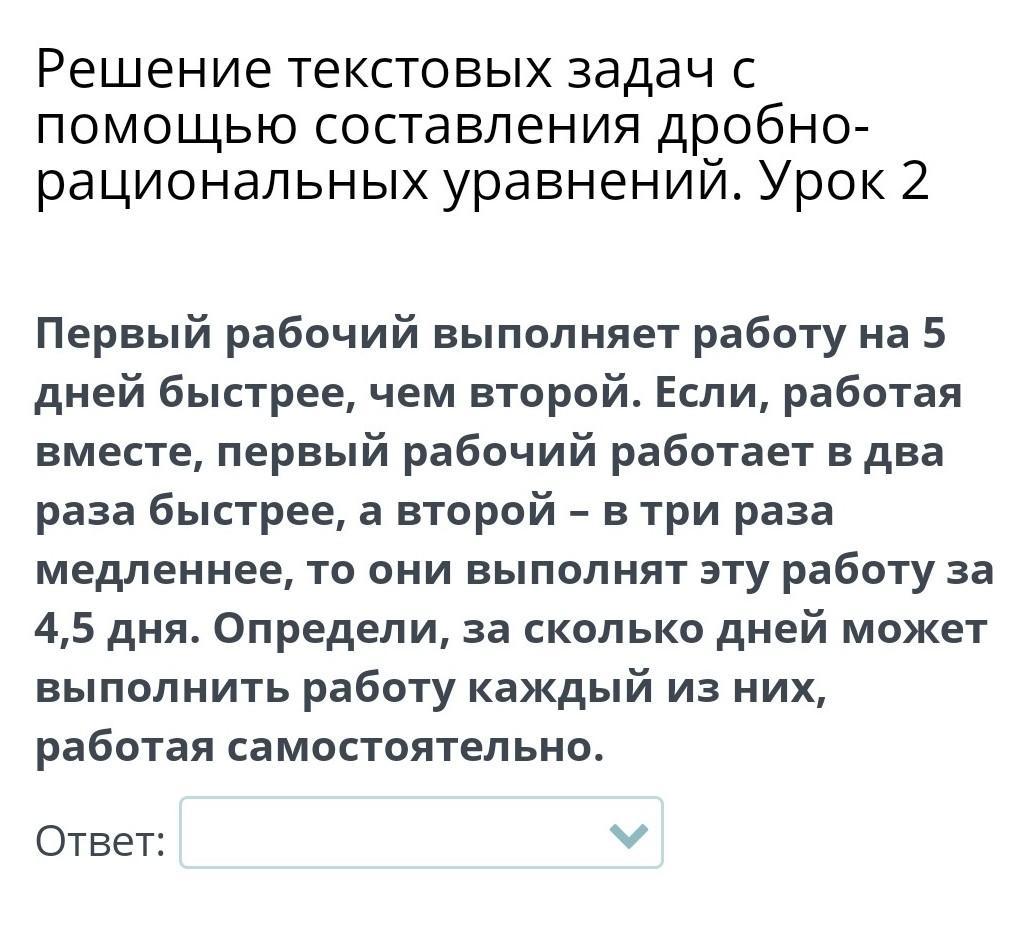
Первый рабочий выполняет работу на 5 дней быстрее, чем второй. Если, работая вместе, первый рабочий работает в два раза быстрее, а второй – в три раза медленнее, то они выполнят эту работу за 4,5 дня. Определи, за сколько дней может выполнить работу каждый из них, работая самостоятельно.​

Answer 1

Обозначим всю работу за 1
Пусть Х - время 1-го рабочего
тогда Х+5 - время 2-го рабочего

1/Х - производительность 1-го рабочего была

1/(Х+5) - производительность 2-го рабочего была

2/Х - производительность 1-го рабочего при совместной работе стала

1/3(Х+5) - производительность 2-го рабочего при совместной работе стала

1/4,5 - общая производительность при совместной работе
Известно , что работая вместе , они выполнят работу за 4,5 дня , т е с производительностью 1/4,5
Составим уравнение:

2/Х + 1/3(Х+5) =1/4,5

4,5*2*(Х+5) + 1,5х = х(Х+5)
9х +45 +1,5х = х^2 +5х
- х^2 +5,5 Х +45 =0 | *(-1)
Х^2 -5,5 Х -45 =0
Д= \| 210,25= 14,5
Х1= (5,5+14,5)/2
Х1= 10 дней - за столько дней выполнит работу 1-й рабочий , работая самостоятельно
Х2= (5,5-14,5)/2
Х2= - 4,5 ( не подходит , не явл корнем)
Х+5=10+5=15 дней - за столько дней выполнит работу 2-й рабочий , работая самостоятельно