Предмет: Математика,
автор: Rich00000000
Помогите решить. Дано комплексное число z. Требуется представить его в
алгебраической, тригонометрической и показательной формах записи.
Приложения:
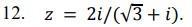
Ответы
Автор ответа:
7
Ответ:
На картинке. В первом домножаем на сопряжённое.
Приложения:

dahhhadd:
чототототочо
мне поставили 3 эххх
писать надо было подробнее, как внизу
Автор ответа:
5
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Yegorpool
Предмет: Английский язык,
автор: Nestlesha
Предмет: Русский язык,
автор: Kanh
Предмет: Математика,
автор: мистер75
Предмет: Физика,
автор: AntyZahvachina