Предмет: Алгебра,
автор: bubblekvas1
ПОМОГИТЕ РЕШИТЬ ПРИМЕР (упростить выражение)
Приложения:
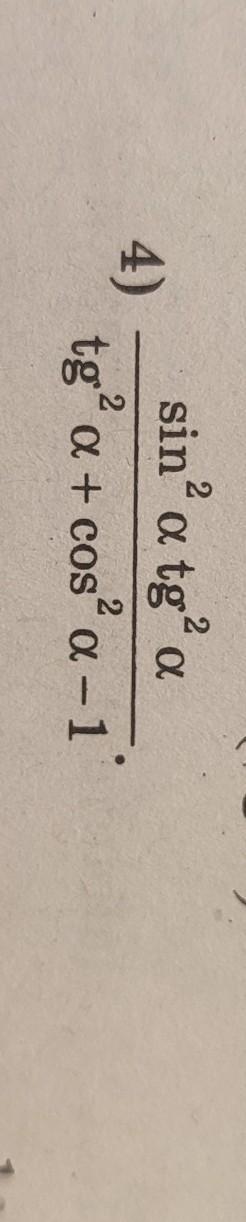
Ответы
Автор ответа:
0
Ответ:
bubblekvas1:
привет,можешь пожалуйста помочь с геометрией, очень прошу у меня самостоятельная работа
в профиле последние 2 вопроса
Похожие вопросы
Предмет: Другие предметы,
автор: KoToLaPa22
Предмет: Английский язык,
автор: Yulya17082012
Предмет: Українська мова,
автор: princeska02
Предмет: Биология,
автор: yashapetrov2016
Предмет: История,
автор: дар123456