Предмет: Алгебра,
автор: wftnxnasz
помогите пожалуйста.
Приложения:
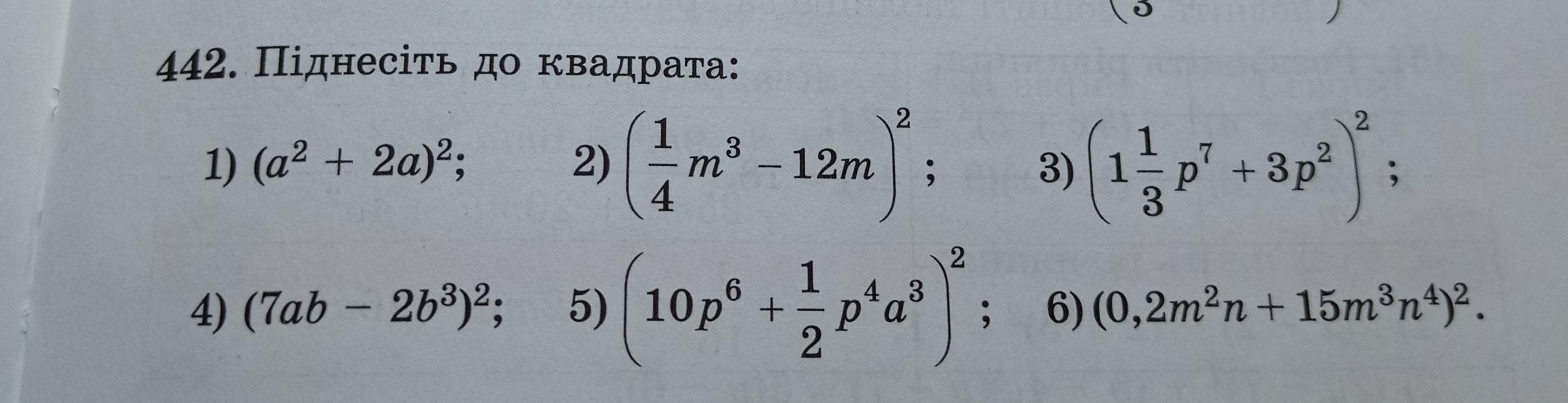
Ответы
Автор ответа:
1
Формулы:
Решение:
Похожие вопросы
Предмет: Технология,
автор: karinaosobole
Предмет: Русский язык,
автор: Малинка1234560
Предмет: Технология,
автор: karinaosobole
Предмет: Английский язык,
автор: lololololo50
Предмет: Математика,
автор: lolipopopok