Предмет: Математика,
автор: mashaefremova6970
найти производную
Y=![\sqrt[8]{x^{3} } -4x^{6} +5In x- 7cos x+tgx+ctg x \sqrt[8]{x^{3} } -4x^{6} +5In x- 7cos x+tgx+ctg x](https://tex.z-dn.net/?f=%5Csqrt%5B8%5D%7Bx%5E%7B3%7D+%7D+-4x%5E%7B6%7D+%2B5In+x-+7cos+x%2Btgx%2Bctg+x)
Ответы
Автор ответа:
1
В основном табличные значения, кроме 1-го. Ну это базовая операция.
Приложения:
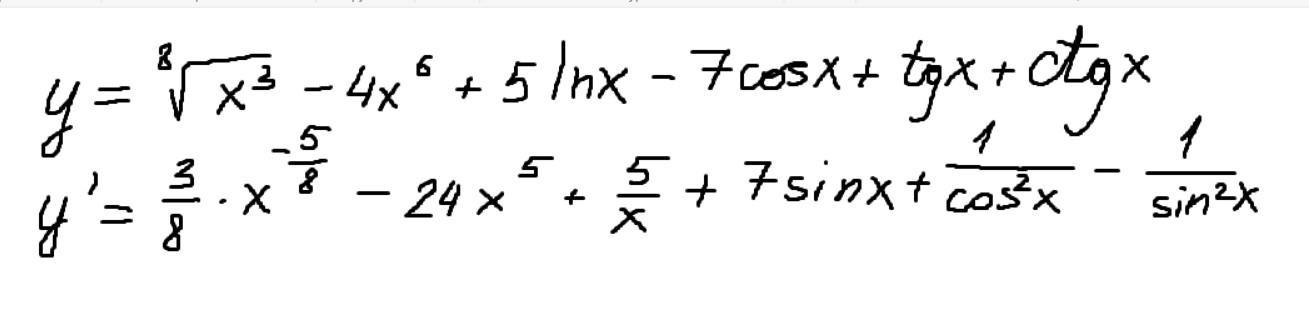
Автор ответа:
1
Формулы:
Используемые формулы:
остальные - табличные.
Решение и ответ:
Похожие вопросы
Предмет: Українська мова,
автор: halukoleh
Предмет: Русский язык,
автор: kokhol88
Предмет: Русский язык,
автор: marinatsymbalo
Предмет: Алгебра,
автор: angelina20080822