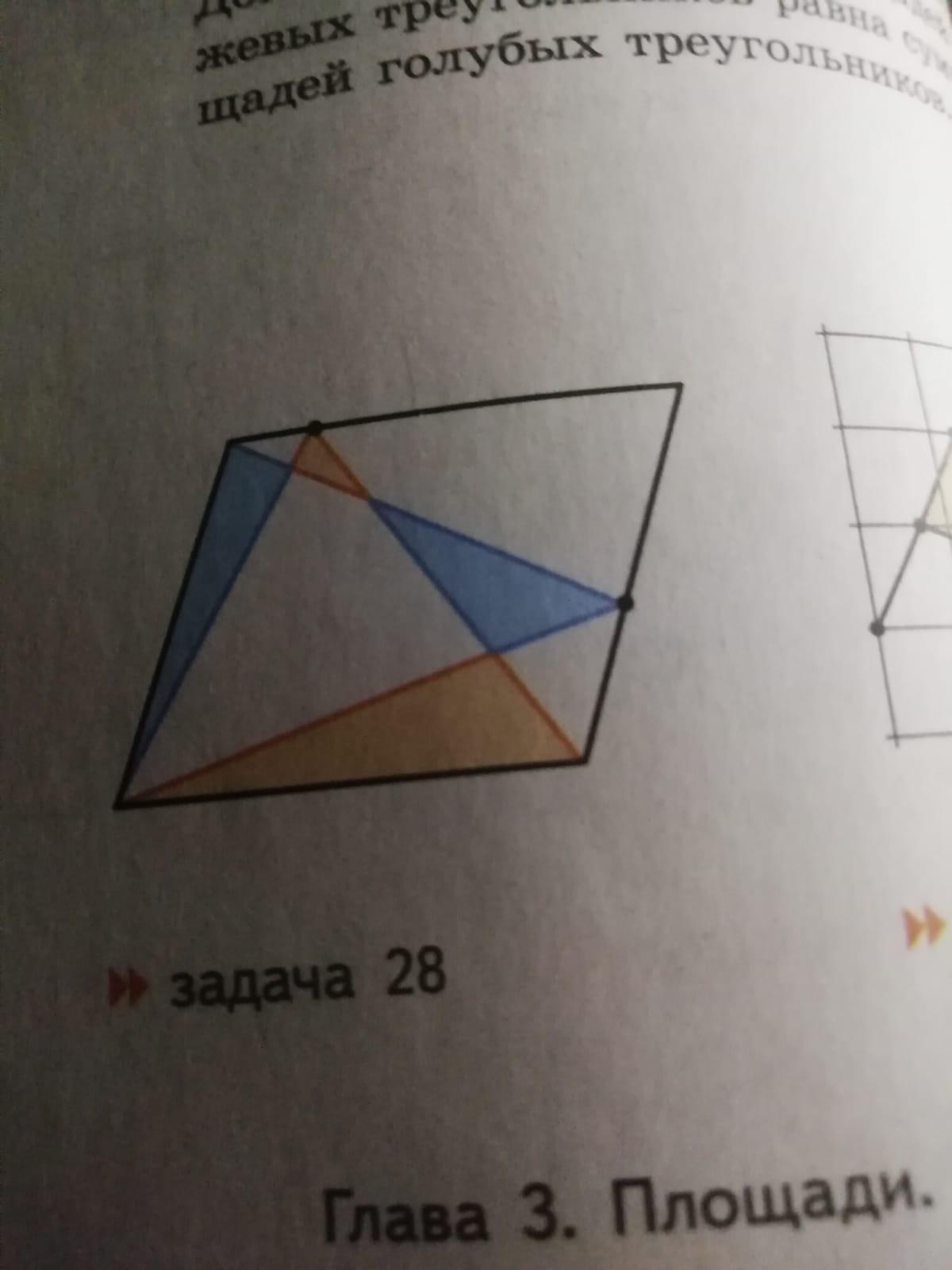
Две точки на сторонах параллелограмма соединили с тремя его вершинами так, как показано на рисунке. Докажите, что сумма площадей оранжевых треугольников равна сумме площадей голубых треугольников. (» рис. )
Ответы
Две точки на сторонах параллелограмма соединили с тремя его вершинами так, как показано на рисунке. Докажите, что сумма площадей оранжевых треугольников равна сумме площадей голубых треугольников.
Объяснение:
Площадь треугольника с синими и белыми частями равна
S( бел часть)+S₁+S₂=1/2*S(паралл.) (*),
а площадь треугольника с синими и желтыми частями равна
S( бел часть)+S₃+S₄=1/2*S(паралл.)(**) .
Тк правые части (*) и(**) одинаковые , то
S( бел часть)+S₁+S₂=S( бел часть)+S₃+S₄ ⇒
S₁+S₂=S₃+S₄ , те сумма площадей оранжевых треугольников равна сумме площадей голубых треугольников.
======================
Если концы одной из сторон параллелограмма соединить с произвольной точкой противоположной стороны , то площадь полученного треугольника равна половине площади параллелограмма.
Доказательство.
S( треуг)=1/2*AD*BH =1/2*(AD*BH)=1/2*S( паралл.)
