Саша любит задачи по комбинаторике, а также любит разгадывать судоку. Однажды он задумался: «Сколькими способами может стоять конкретная цифра в судоку?» Помогите Саше, т.е. укажите сколькими способами можно выбрать 9клеток
доски 9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.
Ответы
Ответ:
Существует 46 656 способов выбрать 9 клеток доски 9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.
Пошаговое объяснение:
Укажите сколькими способами можно выбрать 9 клеток на доске
9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.
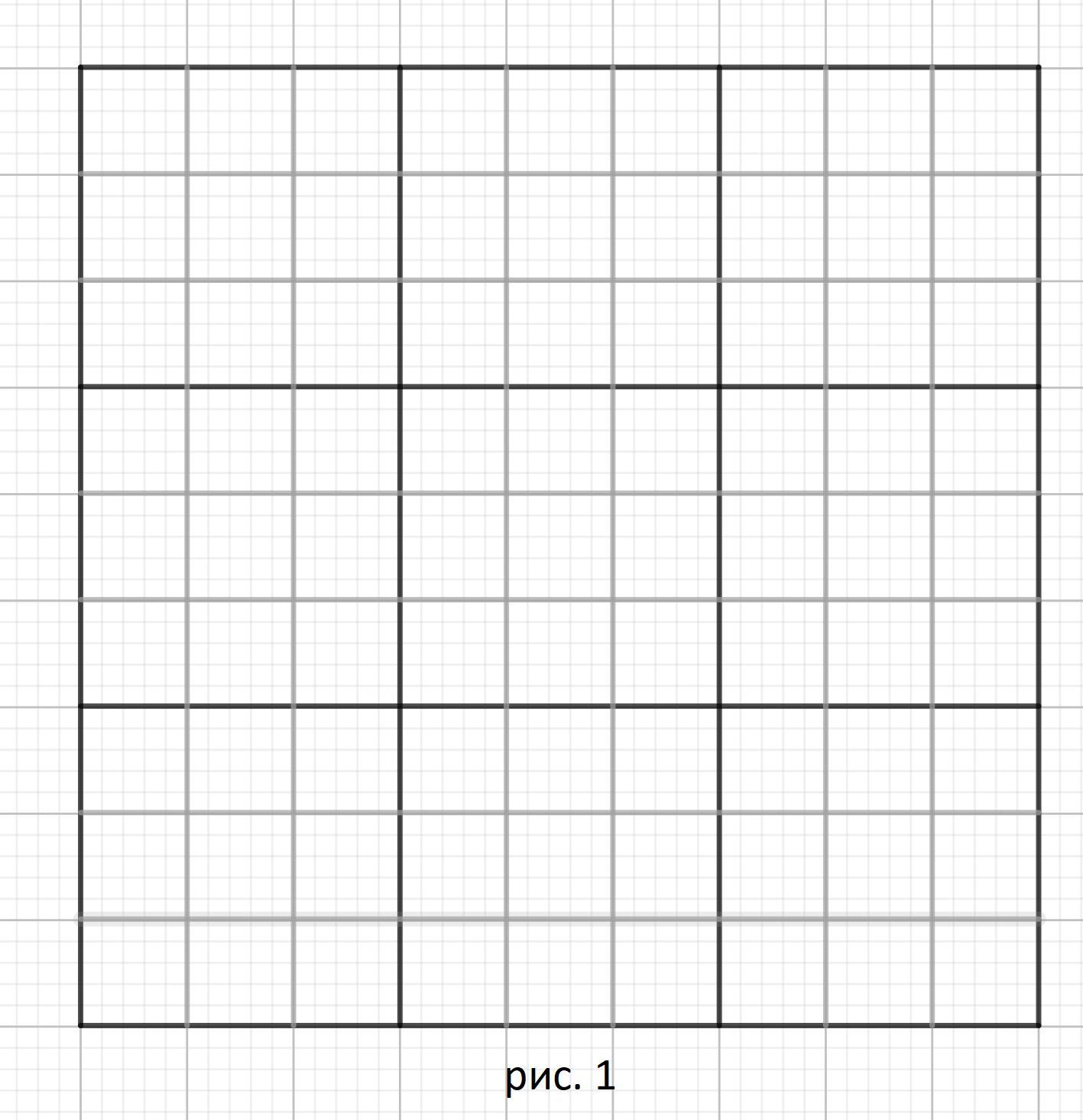
Вспомним как выглядит доска судоку ( рис. 1 во вложении ).
Вся задача сводится к тому , что надо определить сколькими способами можно разместить цифру в одной клетке , в каждом квадратике 3 х 3 соблюдая условие , что в каждом столбце и каждой строчке будет только одна цифра .
Берем первый сверху ряд .
Пусть первая цифра будет стоять в левом верхнем квадрате . В квадрате 9 клеток , надо выбрать одну , значит у нас будет
9 * 1 = 9 способов выбрать эту клетку .
В следующем квадрате 3 х 3 одна строка у нас уже занята , значит 3 клетки мы не можем выбрать , остается 9-3 = 6 клеточек для выбора . Получаем :
6 * 1 = 6 способов выбрать одну клетку .
Переходим в следующий квадрат 3 х 3 . В нем у нас уже две строки заняты , значит мы не можем выбрать :
3 * 2 = 6 клеток , остается
9 - 6 = 3 клетки для выбора . Получаем :
3 * 1 = 3 способа выбрать одну клетку.
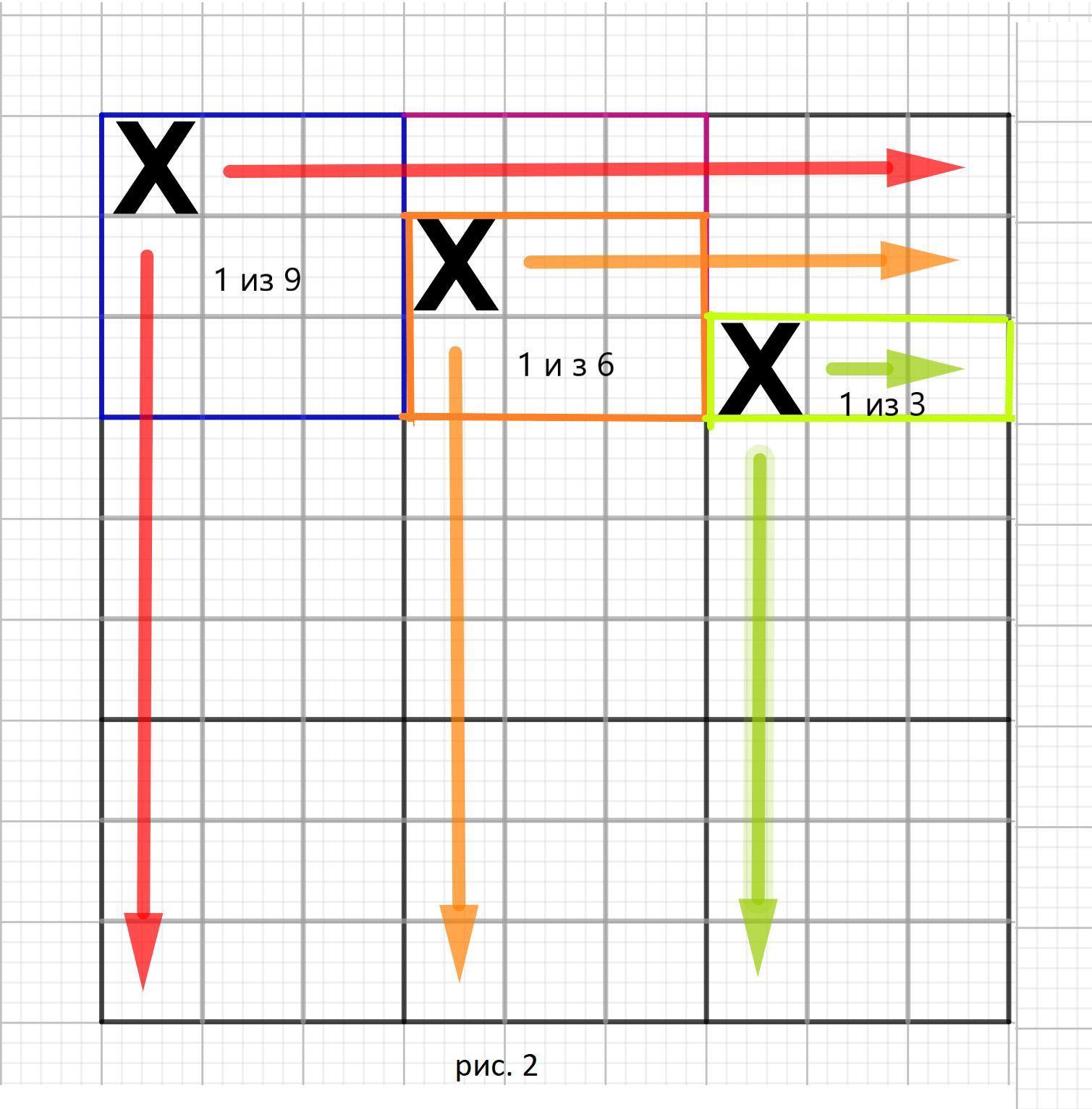
Для наглядности изобразим это на рисунке 2 ( во вложении).
Берем второй ряд.
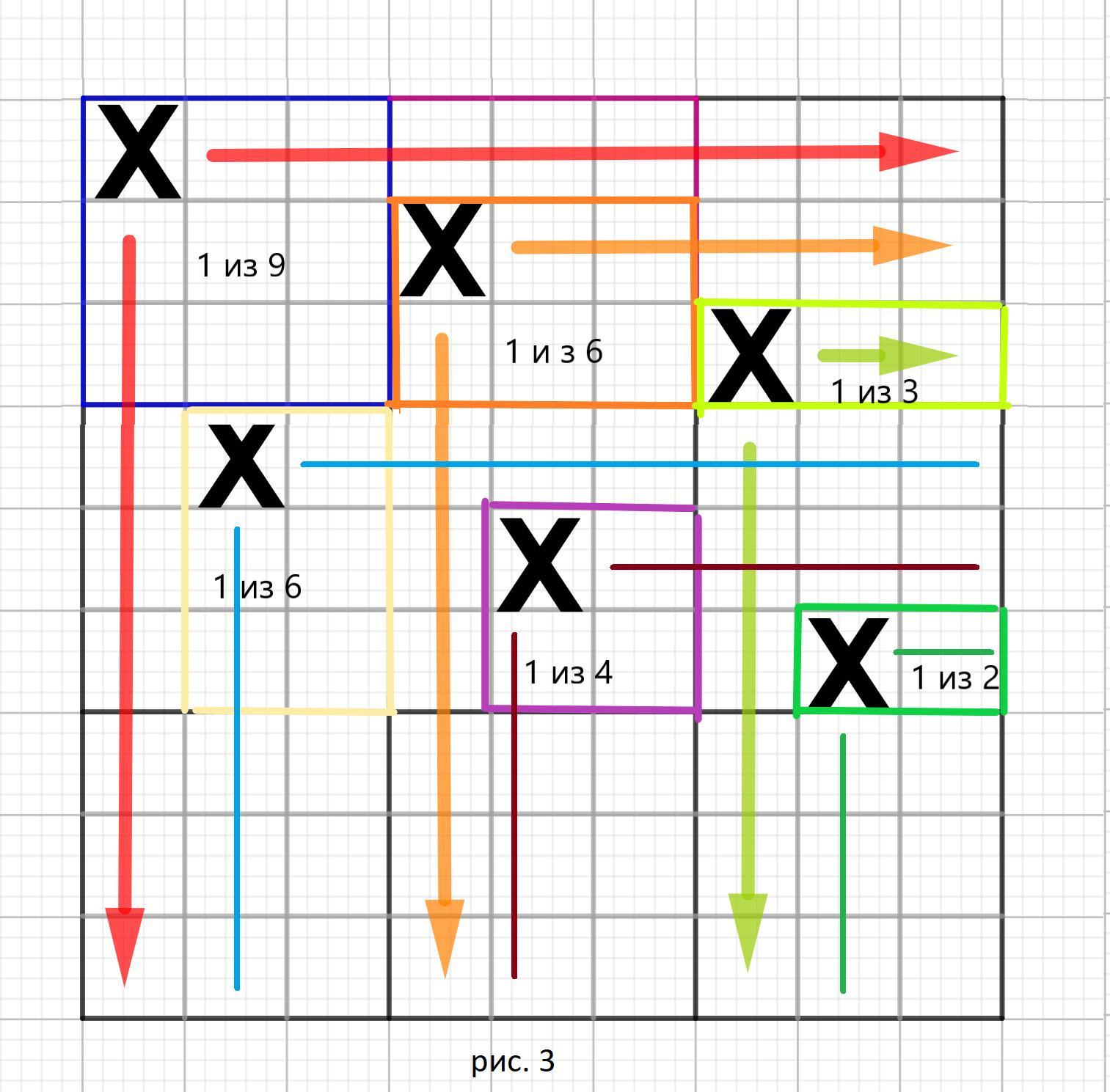
В первом слева квадрате ( рис. 3 во вложении) у нас 3 клетки заняты , значит остается : 9 - 3 = 6 клеток для выбора . Получаем :
6 * 1 = 6 способов выбрать 1 клетку
В следующем квадрате заняты уже 5 клеток ( рис. 3) , остается :
9 - 5 = 4 клетки для выбора . Получаем :
4 * 1 = 4 способа выбрать 1 клетку
В последнем квадрате занято 7 клеток , остается :
9 - 7 = 2 клетки для выбора . Получаем :
2 * 1 = 2 способа выбрать 1 клетку .
Отметим это все на нашем рисунке 3 ( во вложении) .
Переходим к последнему ряду , третьему .
В первом квадрате занято 6 клеток , остается 9 - 6 = 3 клетки для выбора . Получаем :
3 * 1 = 3 способа выбрать 1 клетку
Во втором квадрате занято 7 клеток, остается : 9 - 7 = 2 клетки для выбора и получаем :
2 * 1 = 2 способа выбрать 1 клетку.
В третьем , последнем квадрате нашей доски , свободный остается 1 квадрат , получаем :
1 * 1 = 1 единственный способ выбора клетки.
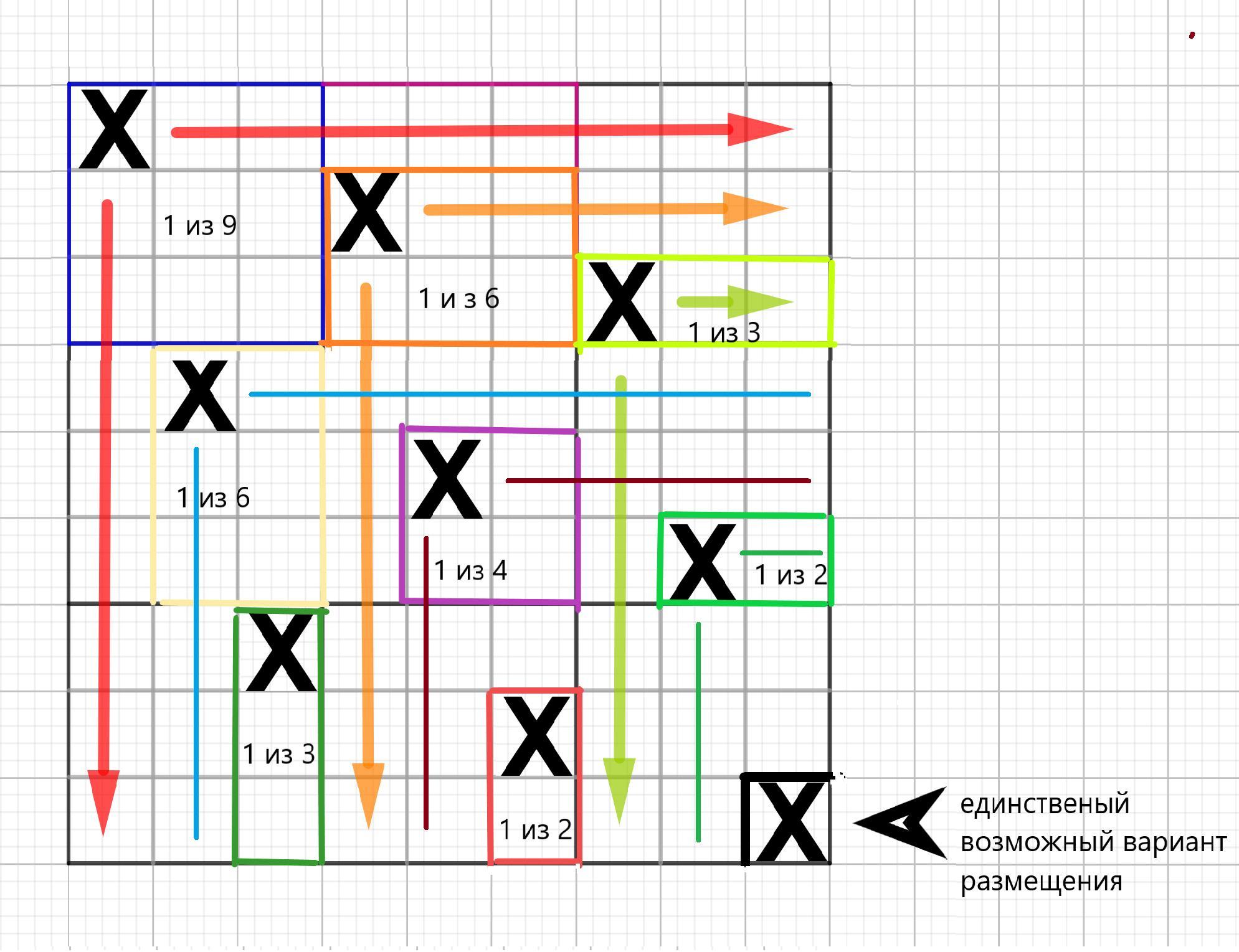
Отмечаем на рисунке 4 ( во вложении)
Мы выбрали 9 клеток , соблюдая условие задачи.
Теперь найдем сколькими способами можно выбрать 9 клеток доски 9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.
По правилу умножения :
9 * 6 * 3 * 6 * 4 * 2 * 3 * 2 * 1 = 46 656 способов.
Существует 46 656 способов выбрать 9 клеток доски 9 х 9, разделенной на девять квадратиков 3 х 3, так, чтобы в каждой строчке, в каждом столбце, и в каждом из девяти квадратиков 3 х 3 была выбрана ровно одна клетка.