Предмет: Алгебра,
автор: linkevicheu
Вычислите площадь фигуры, ограниченной линиями:
y=x ^2 − 4x + 5 и y=x+1
Ответы
Автор ответа:
1
Ответ:
Парабола пересекается с прямой в точках 0 и 4. Ищем площадь на промежутке [0;4]. Т.к прямая находится выше, значит вычитаем из неё параболу.
S = < var > \int\limits^4_0 {(5 - (x^2-4x+5))} \, dx = \int\limits^4_0 {(4x - x^2))} \, dx = 2x^2 - \frac{x^3}{3}|_0^4 = 2 * 4^2 - \frac{4^3}{3} = 10\frac{2}{3} < /var ><var>0∫4(5−(x2−4x+5))dx=0∫4(4x−x2))dx=2x2−3x3∣04=2∗42−343=1032</var> ед^2
Автор ответа:
1
Ответ:
на фото
Объяснение:
все решаем по формулам,ахаха
Приложения:
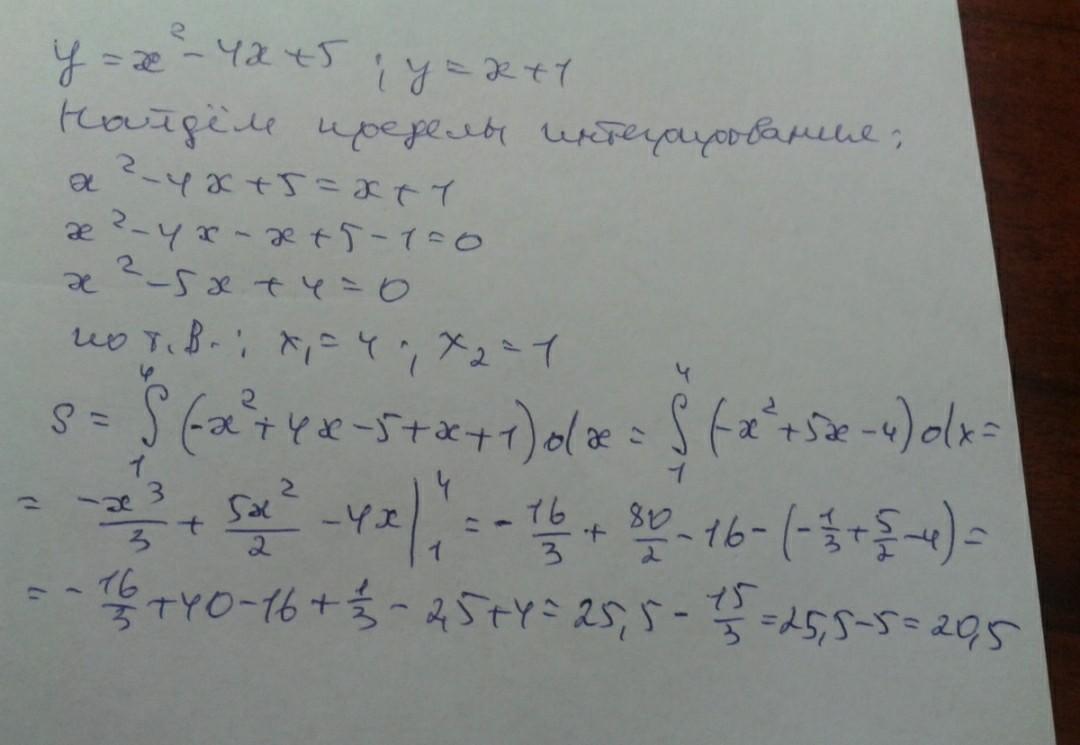
linkevicheu:
x^3=64 ошибочка, но все равно спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: Shamana
Предмет: Українська мова,
автор: FasyAndr
Предмет: Русский язык,
автор: ксю538
Предмет: Русский язык,
автор: ksenVa22