помогите с неравенством
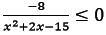
Ответы
Ответ:
х ∈ (-∞; - 5) ∪ (3;+∞).
Объяснение:
Решаем неравенство методом интервалов.
1) Находим нули знаменателя - для этого приравниваем его к 0.
х²+2х-15=0
х₁,₂ = -1±√((-1)² - (-15)) = -1±√16= -1±4
х₁ = -1 - 4 = - 5
х₂ = - 1 + 4 = 3
ОДЗ (область допустимых значений):
х₁ ≠ - 5
х₂ ≠ + 3,
так как при этих значениях знаменатель равен нулю, а на 0 делить нельзя.
2) На числовую ось наносим полученные значения:
- ∞_________-5___________3_________ +∞
Точки -5 и + 3 отмечаем как "выколотые" (значком о) - так как при этих значениях знаменатель превращается в 0, а на ноль делить нельзя.
3) Числовая ось разбита на 3 интервала. Будет проверять знаки функции в каждом интервале, двигаясь справа налево.
4) Проверяем знаки в интервалах:
а) в интервале от +3 до + ∞ выберем, например, точку х = 4, тогда в знаменателе будет 4² + 2 · 4 - 15 = 16 + 8 - 15 = 9 - положительное число; значит, минус в числителе, делённый на минус в знаменателе, даст число отрицательное, то есть дробь будет меньше нуля; значит интервал х∈(3;+∞) нам подходит; в обоих случаях ставим круглые скобки, так как + 3 не может быть решением, согласно ОДЗ, а знак бесконечности всегда закрывается круглой скобкой;
б) в интервале от -5 до 3 возьмём, например, точку х = 0; тогда и числитель, и знаменатель будут отрацательными, а значит дробь - положительной;
в) в интервале от -∞ до -5 возьмём, например, х = -8; в знаменателе будет (-8)²+2 · (-8) - 15 = 64 - 16 - 15 = + 33; значит, дробь будет отрицательной, и интервал х ∈(-∞; - 5) нам подходит.
4) Объединяем области решений и записываем ответ:
х ∈ (-∞; - 5) ∪ (3;+∞).
Ответ: х ∈ (-∞; - 5) ∪ (3;+∞).