Предмет: Геометрия,
автор: 19999megamega19999
Задача написана в закрепе
Приложения:
Ответы
Автор ответа:
0
Ответ:
Объяснение:
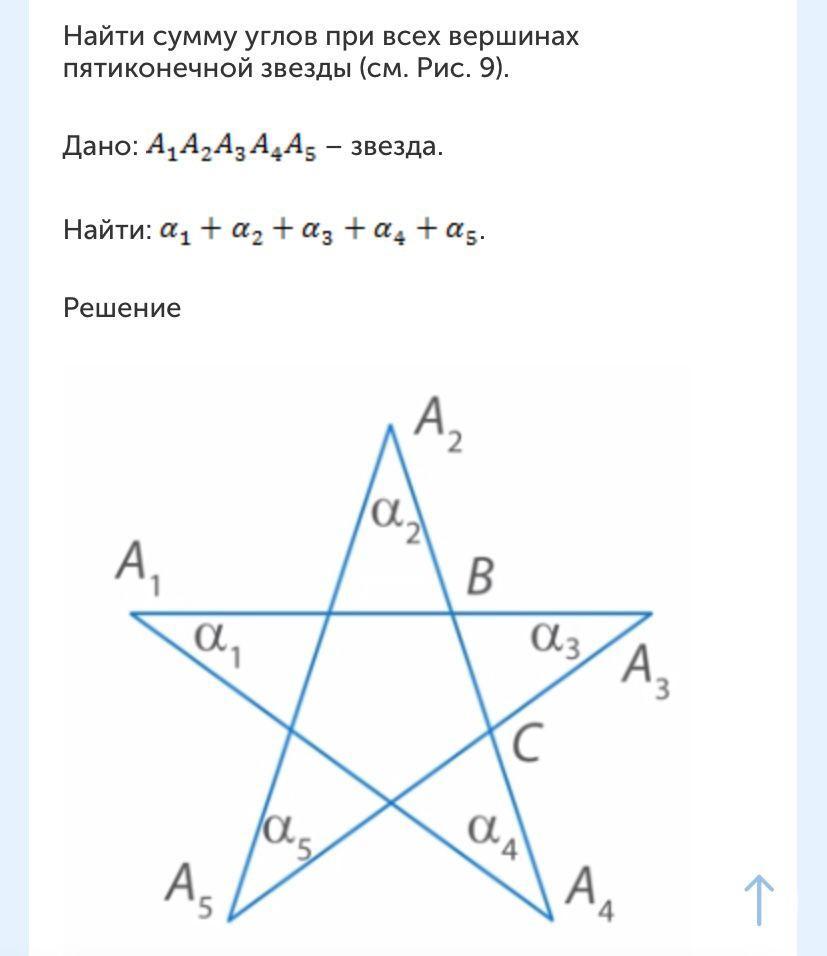
многоугольник внутри звёзды - правильный пятиугольник
угол правильного многоугольника:
- смежные углы
<ВСА=72°
<ВСА=<АВС=72°, =>
<А=36°
Похожие вопросы
Предмет: Окружающий мир,
автор: vainah3376gmailcom
Предмет: Українська мова,
автор: ggez1337
Предмет: Қазақ тiлi,
автор: pazitifion
Предмет: Биология,
автор: dashkazelenskaya2007
Предмет: Окружающий мир,
автор: badretdinovamirbadre