Дана трапеция ABCD с основаниями AD и BC, причём AD = 2BC.
На стороне CD взята точка М. Известно, что DM : MC = 2:3.
а) Докажите, что прямая BM разбивает треугольник ACD на две фигуры,
площади которых относятся как 9 к 46.
б) Найдите площадь четырёхугольника AKMD, где К — точка пересечения
20
—-
3
концами на боковых сторонах трапеции, проходящий через точку
пересечения диагоналей трапеции параллельно её основаниям, равен
22.
Помогите срочно !!!

Ответы
Ответ:
а) Отношение доказано
б) Площадь четырехугольника ед.²
Пошаговое объяснение:
В задаче требуется:
а) Доказать, что прямая ВМ разбивает треугольник ACD на две фигуры, площади которых относятся как 9 : 46.
б) Найти площадь четырёхугольника AKMD.
Дано: ABCD - трапеция;
AD = 2BC - основания;
DM : MC = 2 : 3;
СЕ = - высота;
OН = 22; OН || BC || AD.
a) Доказать:
б) Найти :
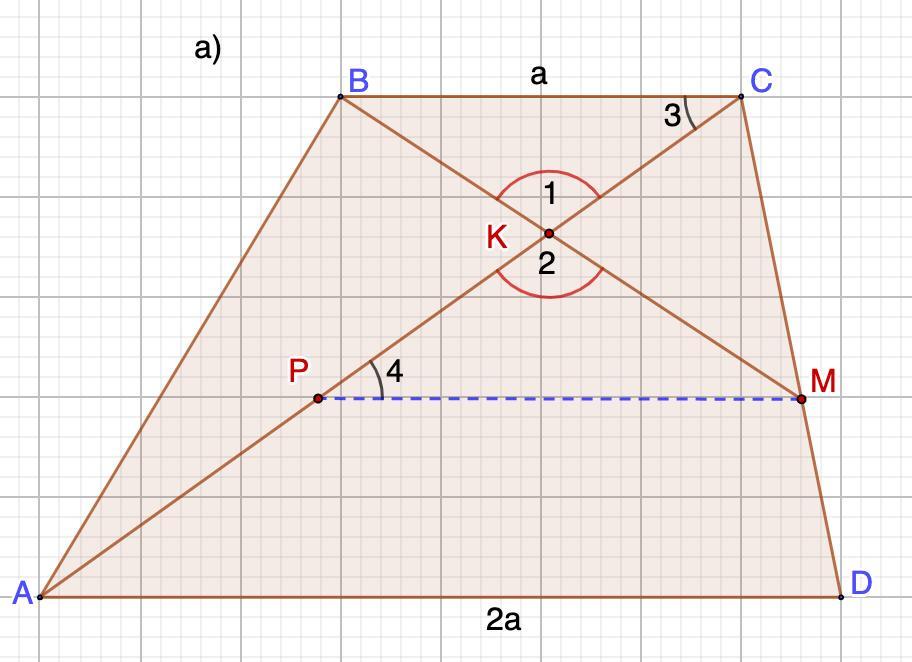
a) Доказательство (рис. а):
Проведем MP || BC || AD.
Пусть ВС = а, тогда AD = 2a.
Пусть DM = 2x, тогда МС = 3х, а CD = 5x.
1. Рассмотрим ∠ACD.
PM || AD (построение);
CM : MD = 3 : 2
- Если параллельные прямые пересекают стороны угла, то отрезки, образовавшиеся на одной стороне угла, пропорциональны соответствующим отрезкам, образовавшиеся на другой стороне угла.
⇒ CP : PA = 3 : 2.
Пусть АР = 2у, тогда СР = 3у, a AC = 5y.
2. Рассмотрим ΔACD и ΔРСМ.
РМ || AD (построение)
- Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.
⇒ ΔACD ~ ΔРСМ.
Запишем отношение сходственных сторон и найдем РМ:
3. Рассмотрим ΔКВС и ΔРКМ.
∠1 = ∠2 (вертикальные)
∠3 = ∠4 (накрест лежащие при ВС || РМ и секущей РС)
⇒ ΔКВС ~ ΔРКМ (по двум углам)
Запишем отношение сходственных сторон:
⇒ СК = 5 частей, КР = 6 частей, а СР = 11 частей.
С другой стороны СР = 3у
Выразим СК:
4. Выразим площади.
Воспользуемся формулой:
, где a и b - стороны треугольника; α - угол между ними.
Найдем площадь AKMD:
5. Найдем искомое отношение:
⇒ Что и требовалось доказать.
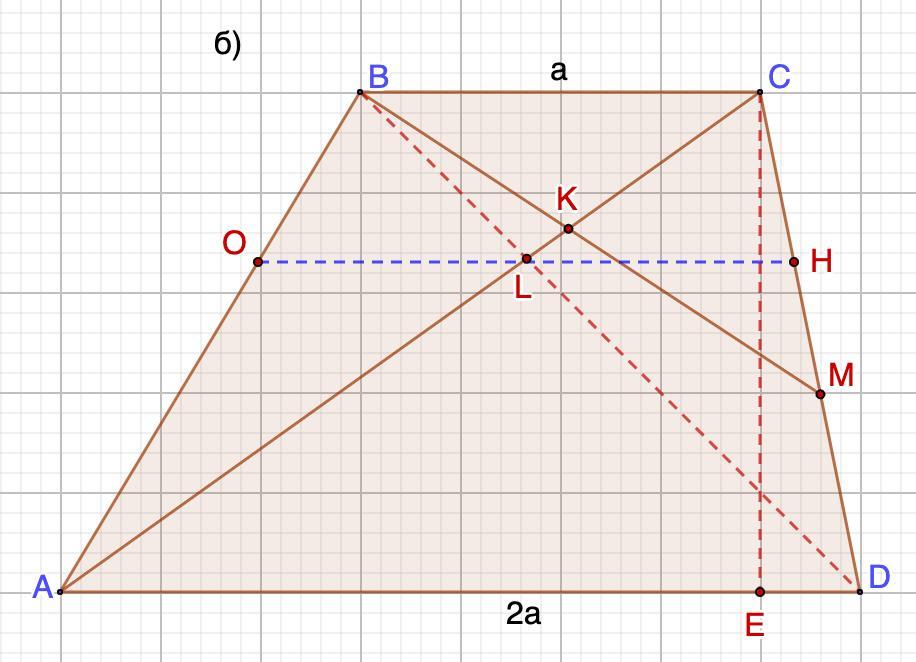
б) Решение (рис. б)
1. Рассмотрим ΔBCL и ΔALD.
∠BLC = ∠ALD (вертикальные)
∠ВСL = ∠LAD (накрест лежащие при BC || AD и секущей АС)
⇒ ΔBCL ~ ΔALD (по двум углам)
Запишем отношение сходственных сторон:
2. Рассмотрим ΔAOL и ΔABC
OL || BC (условие)
⇒ ΔAOL ~ ΔABC (лемма)
Запишем отношение сходственных сторон и найдем OL:
3. Рассмотрим ΔLCH и ΔACD
HL || AD (условие)
⇒ ΔLCH ~ ΔACD (лемма)
Запишем отношение сходственных сторон HL:
4. OH = OL + LH
5. Зная основание и высоту, найдем площадь ΔACD по формуле:
, где a и h -основание и высота соответственно.
6. Из пункта а) знаем отношение
То есть, на приходится 46 частей, ⇒ на
- (46+9) = 55 (частей)
Можем найти искомую площадь :
(ед²)
Площадь искомого четырехугольника S (AKMD) = 92 (ед².)