Question

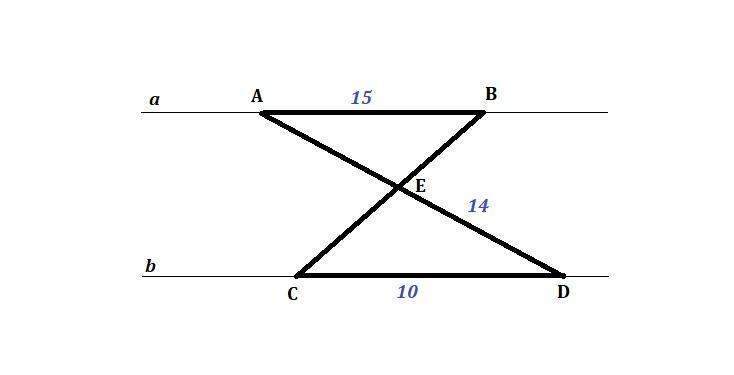
a||b, AB принадлежит a, CD принадлежит b,AD пересек BC=Е. Найдите долину отрезка AD,если DE=14 CD=10 AB=15

Answer 1

Ответ:

AD = 35 см

Объяснение:

Так как a || b, AB ∈ a, CD ∈ b, то AB || CD.

Рассмотрим ΔАВЕ и ΔDСЕ.

∠АВЕ = ΔDЕС - как внутренние накрест лежащие углы при параллельных прямых AB и CD и секущей ВС;

∠АЕВ = ∠DЕС - как вертикальные.

Следовательно ΔАВЕ подобен  ΔDСЕ по двум углам (первый признак подобия)

Из подобия треугольников следует пропорциональность соответствующих сторон:

$\dfrac{AB}{DC} =\dfrac{AE}{DE} \\\\ \\ \dfrac{15}{10} =\dfrac{AE}{14}\\ \\\\ AE=\dfrac{15*14}{10} = 21$ см

AD = AE + DE = 21 + 14 = 35 cм