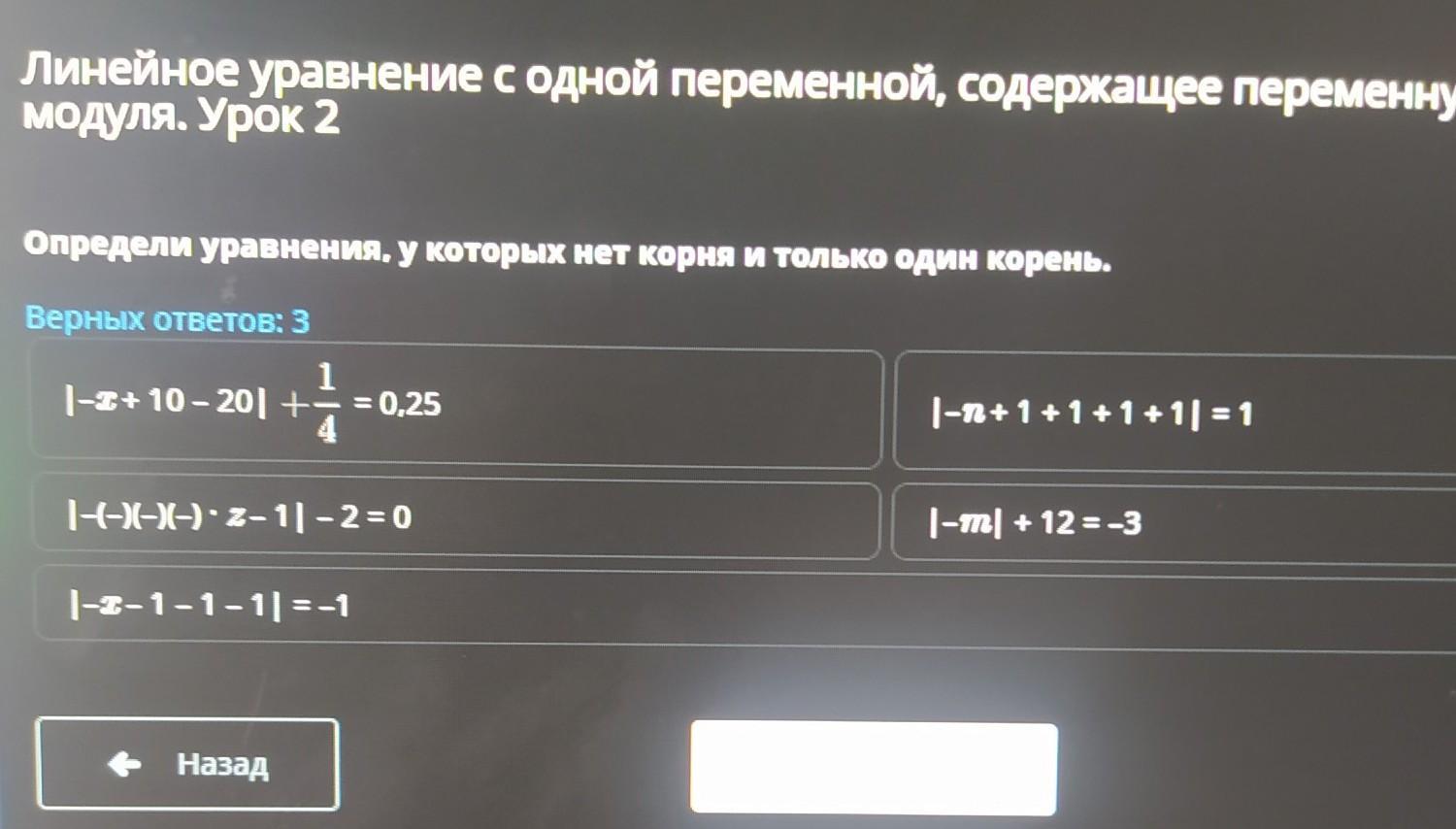
Определи уравнения, у которых нет корня и только один корень. Верных ответов: 3 |-x + 10 - 20| + 1/4 = 0,25 |-(-)(-)(-) • z - 1| - 2 = 0 |-x-1-1-1| = -1 |-n +1+1+1+1| = 1 |-m|+12= -3
Ответы
Ответ:
Нет корней в уравнениях :
| -x - 1 - 1 - 1 |= -1
| -m | + 12 = - 3
Один корень в уравнении :
Пошаговое объяснение:
Определи уравнения, у которых нет корня и только один корень.
Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным.
1. Модуль положительного числа равен самому числу.
|a| = a, если a > 0
2. Модуль отрицательного числа равен противоположному числу.
|−a| = a
3. Модуль нуля равен нулю.
|0| = 0, если a = 0
Решим уравнения и найдем те у которых нет корня или он только один.
1)
тогда получим :
| - x -10 | + 0,25= 0,25
|- x - 10 | = 0,25 - 0,25
| - x - 10 | = 0
Раскроем модуль :
- х - 10 = 0
- х = 10
х = - 10
уравнение имеет только один корень .
2) | - ( - ) ( - ) ( - ) *z - 1 | - 2 = 0
разберемся с минусами, их 4 , четное число , значит в результате получим положительное число :
| z - 1 | = 2
при раскрытии модуля получим два уравнения :
z - 1 = 2 или z - 1 = - 2
z = 2 + 1 z = - 2 + 1
z = 3 z = -1
уравнение имеет два корня .
3) | -x - 1 - 1 - 1 |= -1
уравнение не имеет корней , поскольку модуль не может быть отрицательным числом
4)
| -n + 1 + 1 + 1 + 1 |= 1
| - n + 4 | = 1
раскроем модуль и получим два уравнения
- n + 4 = 1 или - n + 4 = -1
n = 3 n = 5
уравнение имеет два корня
5)
| -m | + 12 = - 3
| - m | = -3 -12
| - m | = - 15
уравнение не имеет корней , поскольку модуль не может быть отрицательным числом