Предмет: Геометрия,
автор: grigorevalana27
ПОЖАЛУЙСТА ПОМОГИТЕ, СРОЧНО. Площадь ромба равна 540 см2, а одна из его диагоналей равна 4,5 дм. Найдите расстояние от точки пересечения диагоналей до стороны ромба.
Ответы
Автор ответа:
0
Ответ:
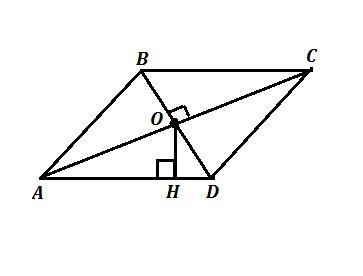
S(ромба)=540 см² , d₁=AC=4,5 дм=45 см , точка О - точка пересечения диагоналей ромба , ОН⊥AD . Найти ОН .
Площадь ромба равна ,
см
Так как диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам, то АО=ОС=45:2=22,5 см , ВО=ОD=24:2=12 см , и ΔAOD - прямоугольный, поэтому
,
см .
Для ΔАОD запишем, чему равна его площадь .
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Juliy336
Предмет: Английский язык,
автор: DJboy281
Предмет: Русский язык,
автор: misterkeks
Предмет: Химия,
автор: Evdokimova02
Предмет: Алгебра,
автор: milenasalikova