Предмет: Алгебра,
автор: aallllll
Помогите пожалуйста решить
Приложения:
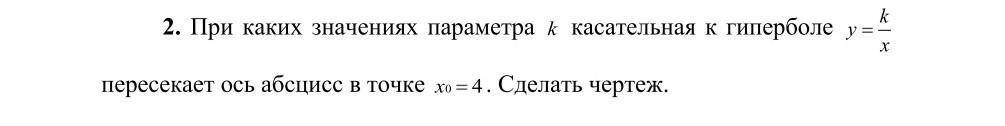
Ответы
Автор ответа:
1
Объяснение:
Прямая, проходящая через точку (4;0) в точке касания с гиперболой у=к/х (к - угловой коэффициент) перпендикулярна ей, является нормалью и описывается уравнением:
Нормаль и гипербола имеют одну общую точку (точку касания) ⇒
Это уравнение имеет одно решение. ⇒
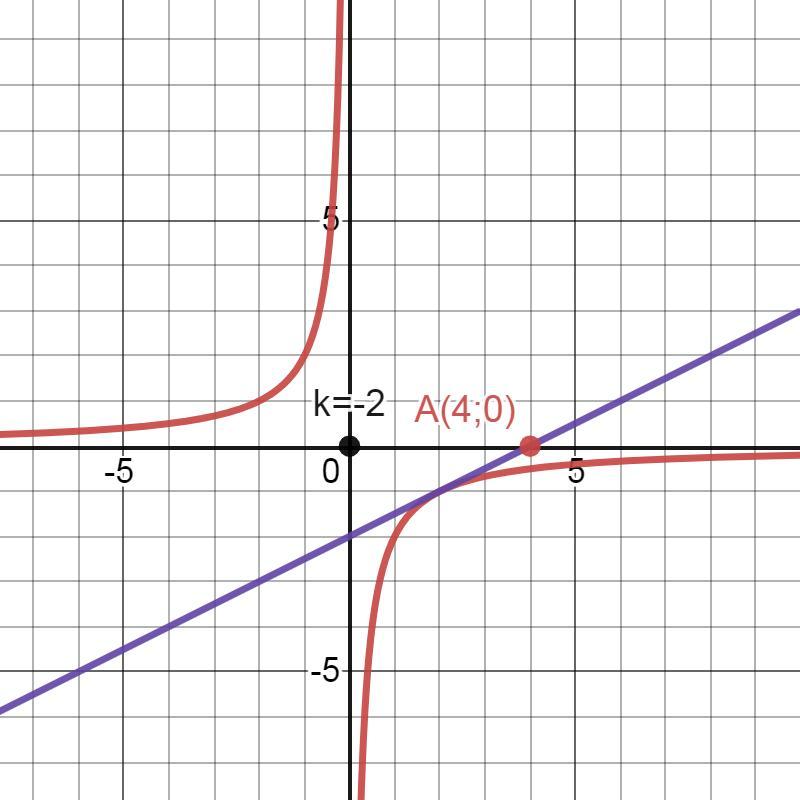
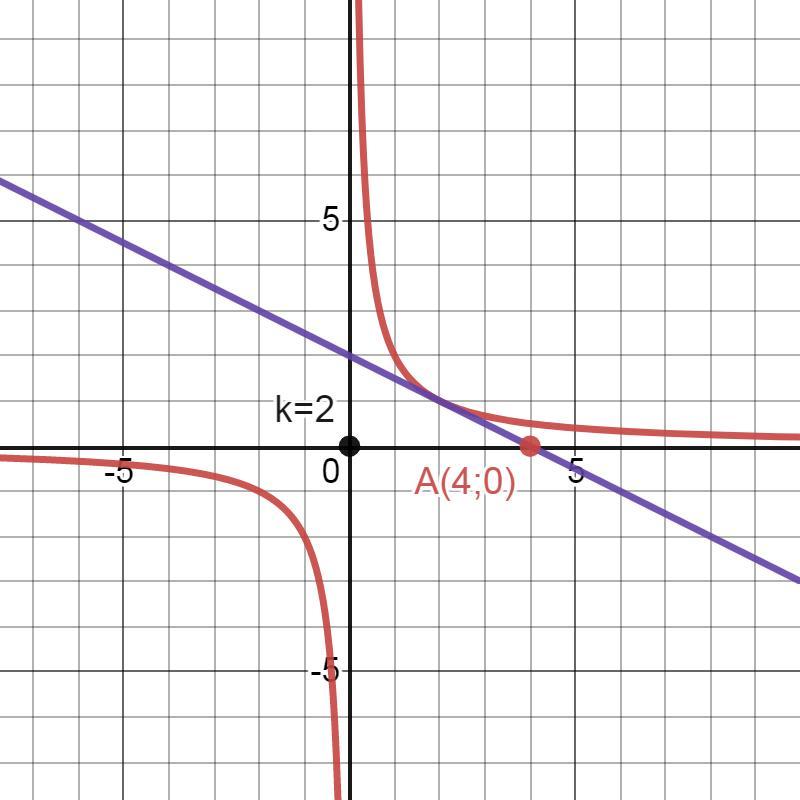
Ответ: к₁=-2 к₂=2.
Приложения:
aallllll:
спасибо большое
а вы знаете "управление затратами"?
Давайте задание. Попробую решить.
посмотрите добавил
ну так что
Похожие вопросы
Предмет: Английский язык,
автор: qwerqwer123456
Предмет: Русский язык,
автор: 213451
Предмет: Русский язык,
автор: Единорого
Предмет: Химия,
автор: NikNek228
Предмет: Английский язык,
автор: I77Egor77I