Предмет: Алгебра,
автор: aallllll
Помогите пожалуйста решить
Приложения:

Ответы
Автор ответа:
1
Приложения:
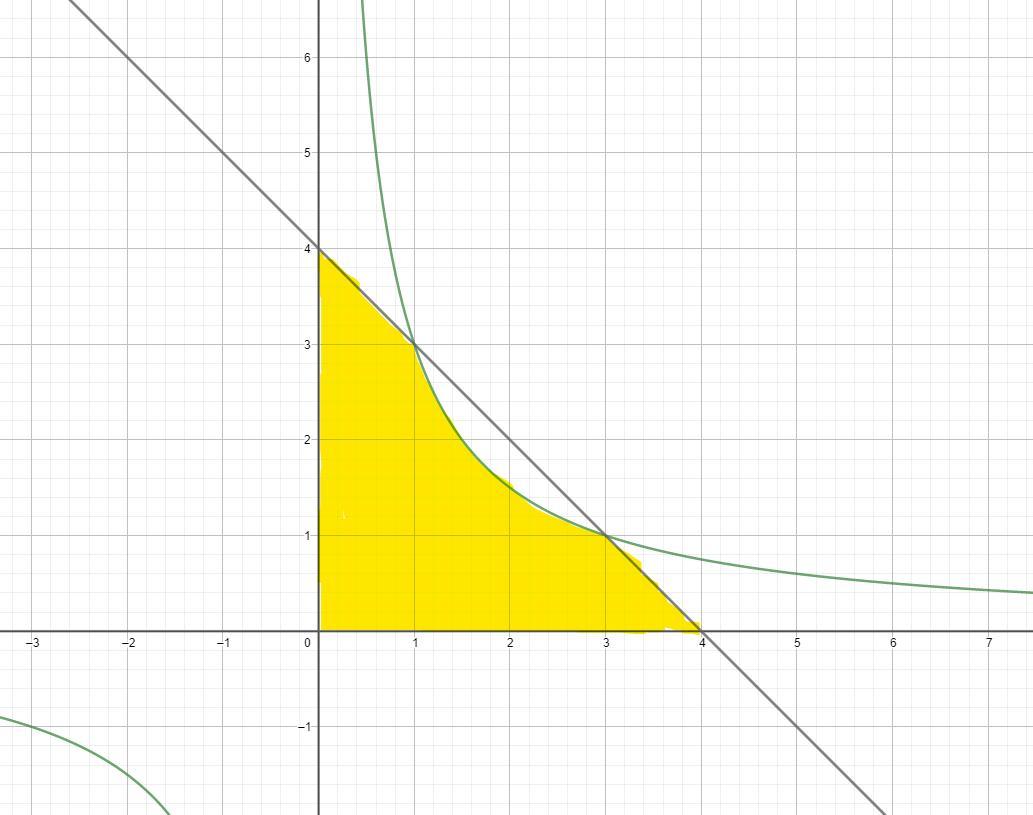
aallllll:
спасибо большое
если свабодны еще помогите)
Похожие вопросы
Предмет: Другие предметы,
автор: RussMan
Предмет: Русский язык,
автор: alenaalena000
Предмет: Английский язык,
автор: Ardnaskela228
Предмет: Алгебра,
автор: maslovan