помогите, пожалуйста
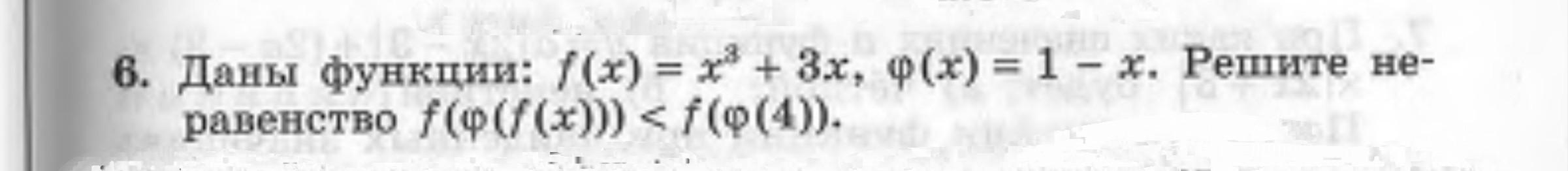
Ответы
Ответ: x > 1 або xЄ ( 1 ; + ∞ ) .
Объяснение:
f( x ) = x³ + 3x ; φ( x ) = 1 - x ; нерівність f( φ( f( x ))) < f( φ( 4 )) ;.
Запишемо складені функції :
1) φ( f( x )) = 1 - ( x³ + 3x ) = - x³ - 3x + 1 ;
f( φ( f( x ))) = (- x³ - 3x + 1 )³ + 3*(- x³ - 3x + 1 ) ;
2) φ( 4 ) = 1 - 4 = - 3 ;
f( φ( 4 )) = f(- 3 ) = (- 3 )³ + 3*(- 3 ) = - 27 - 9 = - 36 .
Підставимо функції у задану нерівність :
(- x³ - 3x + 1 )³ + 3*(- x³ - 3x + 1 ) < - 36 ;
заміна t = - x³ - 3x + 1 ; маємо :
t³ + 3t + 36 < 0 ; підбір дає нам корінь t = - 3 , тоді
( t + 3 )( t² - 3t + 12 ) < 0 .
Дискримінант 2 - го множника від"ємний , а а > 0 , тому він
для будь- яких х приймає тільки додатні значення . Поділимо
на нього нерівність :
t + 3 < 0 . Повернемося до змінної х :
- x³ - 3x + 1 + 3 < 0 ; або
x³ + 3x - 4 > 0 . Тричлен має корінь х = 1 ( теж підбором ) :
( x - 1 )( x² + x + 4 ) > 0 .
Дискримінант 2 - го множника від"ємний , а а > 0 , тому він
для будь- яких х приймає тільки додатні значення . Поділимо
на нього нерівність :
x - 1 > 0 ;
x > 1 ; xЄ ( 1 ; + ∞ ) .
В - дь : x > 1 або xЄ ( 1 ; + ∞ ) .