Question

в прямоугольном треугольнике больший катет на 1 см меньше гипотенузы,а меньший катет на 32 см меньше гипотенузы. найди стороны треугольника ​

Answer 1

Ответ:

9см, 40см, 41 см

Объяснение:

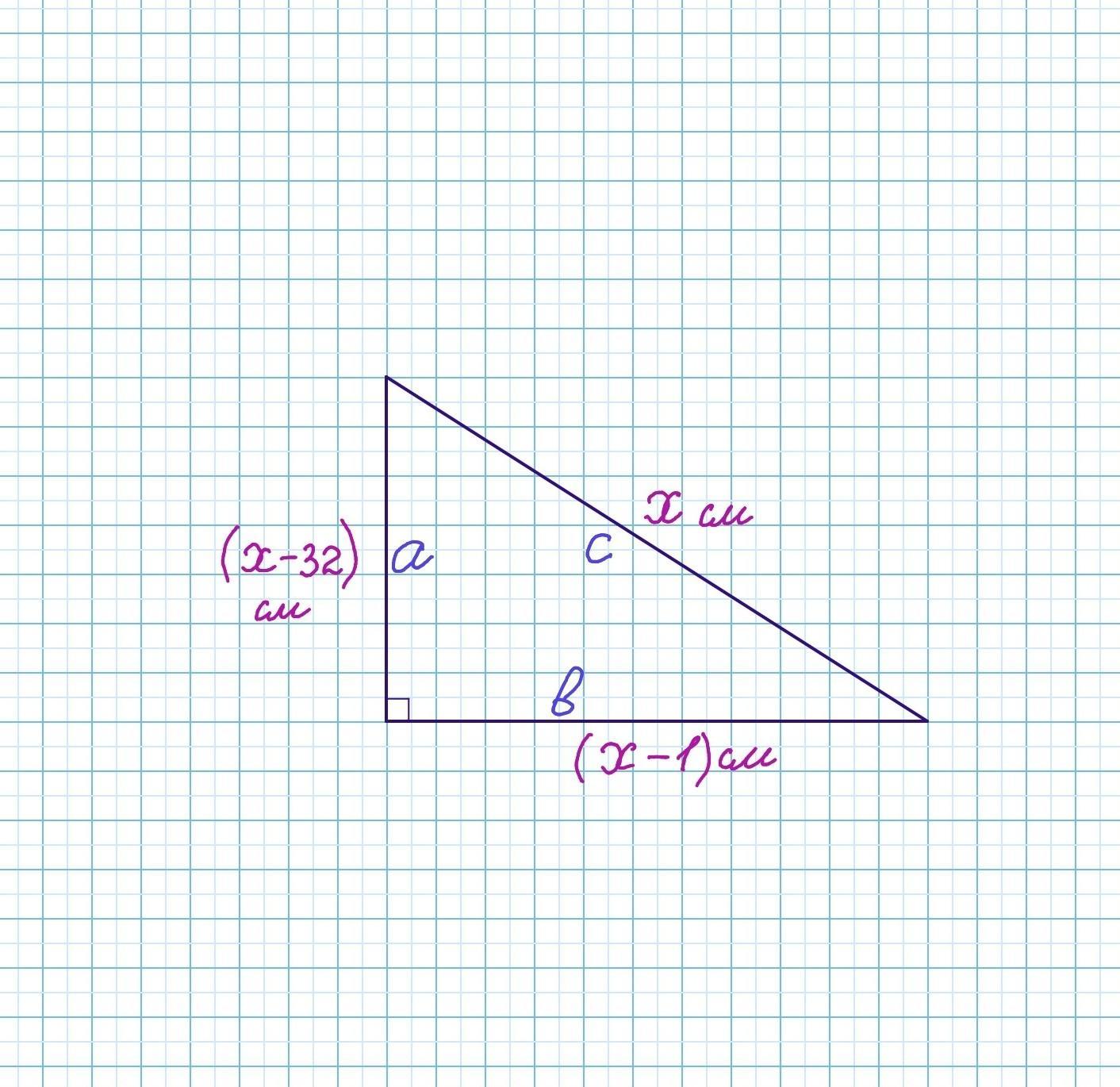
Пусть гипотенуза с равна х см. Тогда меньший катет а равен (х-32) см, а больший катет b равен (х-1) см.

По теореме Пифагора квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов:

${a}^{2} + {b}^{2} = {c}^{2} \\ \\ ({x - 32})^{2} + ({x - 1})^{2} = {x}^{2} \\ \\ {x}^{2} - 64x + 1024 + {x}^{2} - 2x + 1 - {x}^{2} = 0 \\ \\ {x}^{2} - 66x + 1025 = 0 \\ \\ d = {b}^{2} - 4ac = {66}^{2} - 4 \times 1025 = 4356 - 4100 = 256 = {16}^{2} \\ \\ x_1 = \dfrac{ - b + \sqrt{D} }{2a} = \dfrac{ 66 + 16}{2} = 41 \\ \\ x_2 = \dfrac{ - b - \sqrt{D} }{2a} = \dfrac{66 - 16}{2} = 25$

$x_2=25$ - не подходит, т.к. в этом случае меньший катет будет меньше нуля:

х-32 = 25-32 = -7

Поэтому гипотенуза с = 41 см, катет а = х-32 = 41-32 = 9 см, катет b = x-1 = 41-1 = 40 см