Предмет: Геометрия,
автор: FaerVator
Тема: Теорема синусов.
Задание: В треугольнике с углами 105° и 45° наименьшая сторона равна 4√2 см. Найдите среднюю по длине сторону этого треугольника.
Ответы
Автор ответа:
7
Ответ:
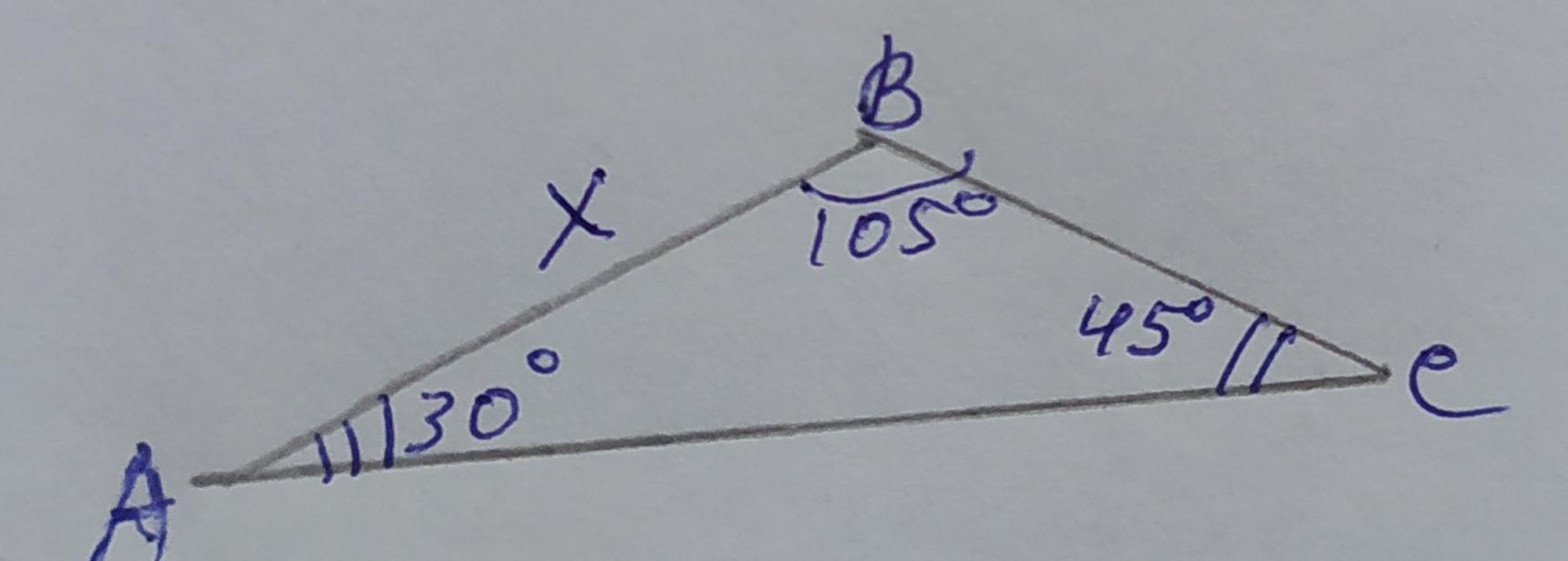
Обозначим вершины треугольника А В С. Пусть ∠В=105°. Сумма углов треугольника равна 180°. Найдём неизвестный угол: 180–105–45=30°. Тогда самый меньший угол – это ∠А=30°, а средний – это ∠С=45°. Напротив меньшего угла лежит наименьшая сторона поэтому ВС=4√2, так как лежит напротив ∠30°. Средняя сторона – это сторона АВ, так как лежит напротив ∠С=45°, обозначим АВ=х и применим теорему синусов:
перемножим крест на крест:
х•sin30°=4√2•sin45°
х•1/2=4√2•√2/2
х•1/2=4×2/2
х•1/2=4
х=4÷1/2
х=4×2
х=8 см – искомая сторона АВ
ОТВЕТ АВ=8см
Приложения:
FaerVator:
спасибо большое ))
Рада, что помогла)
Похожие вопросы
Предмет: Русский язык,
автор: ранатур
Предмет: Английский язык,
автор: ЕлизаветаПропик
Предмет: Русский язык,
автор: lerchik151
Предмет: Русский язык,
автор: Ustailia
Предмет: Английский язык,
автор: norri